이하은 , 김지호 , 경수아 , 김효경 , 정영민 , 박정도 , 김지웅
탄소 섬유 강화 세라믹 매트릭스로서 312 MAX 상의 적합성 평가:제1원리 계산
Ab initio Calculations of 312 MAX Phases as Matrix for Carbon Fiber Reinforced Ceramics
Haeun Lee, Jiho Kim, Sooah Kyung, Hyokyeong Kim, Youngmin Jeong, Jungdo Park, Jiwoong Kim
Abstract: Carbon fiber reinforced ceramics (CFRCs) are well-suited for aerospace components due to their high-temperature stability and oxidation resistance. The SiC-based matrix offers excellent fracture toughness and thermal shock resistance but is prone to defects such as cracking and delamination due to its brittleness. To address these issues, ongoing research focuses on incorporating MAX phase ceramics into composites. In this study, tailoring the M-site composition in MAX phases, such as M 3 SiC 2 structures, expands the mechanical and thermal properties using ab initio calculations. This study identified that Ta-based M 3 SiC 2 MAX phases exhibit high bulk modulus, making them resistant to pressure changes, while Ti and Hf-based phases demonstrate high shear and Young’s modulus, contributing to superior crack resistance and thermal durability. Additionally, Ti, Zr, Hf, and Ta-based compositions were found to have thermal expansion properties like SiC f effectively mitigating thermal stress and fatigue under rapid temperature fluctuations. Ab initio calculations identified Ti, Zr, Hf, and Ta-based M 3 SiC 2 MAX phases as the most promising matrix materials for CFRCs in aerospace and high-temperature applications.
Keywords: Ab initio calculation , aerospace , carbon fiber reinforced ceramics , MAX phase , mechanical property
1. 서 론
항공우주 분야에서 극한 환경에 적합한 소재 개발은 산업 전반에서 중요한 연구 분야로 자리잡고 있다. 항공기, 우주선, 엔진, 로켓 부품 등은 고온, 고압, 방사선, 산화 조건 등 다양한 극한 환경에서 작동해야 한다[1]. 이러한 극한 환경에서는 소재가 단순히 물리적 구조를 유지하는 것 이상의 성능을 요구하며, 장기간의 내구성, 강도, 열적 안정성 등이 필수적이다[2]. 특히, 우주와 항공 환경은 높은 온도 변화, 진공 상태, 우주 방사선 등의 극단적인 조건을 포함하므로, 소재가 이러한 조건에서도 안정적이고 효율적으로 작동해야 한다[3]. 이러한 요구를 충족하는 소재를 개발하는 것은 항공우주 기술의 발전을 위한 중요한 과제이다.
기존의 금속 및 세라믹 소재는 일부 극한 조건에서는 우수한 성능을 보이지만, 장기간 사용에 있어 높은 비용, 열적 피로, 구조적 변형 등으로 한계를 드러낸다[4]. 특히, 이러한 소재는 고온 환경에서 강도와 안정성을 유지하기 어렵고, 반복적인 하중이나 열적 충격으로 인한 물리적 손상이 발생할 수 있다[5]. 이러한 문제를 해결하기 위해 항공 우주 분야에서는 복합재료가 주목받고 있다. 그 중에서도 carbon fiber reinforced ceramics (CFRCs)는 고온 및 고압 환경에서의 성능을 개선할 수 있는 유망한 대안으로 떠오르고 있다[6].
CFRCs는 탄소 섬유(carbon fiber, [TeX:] $$\mathrm{C}_{\mathrm{f}}$$) 또는 SiC 섬유([TeX:] $$\mathrm{SiC}_{\mathrm{f}}$$)와 SiC 매트릭스(matrix)를 조합한 복합재료이다. 항공우주 분야에서 뛰어난 내산화성, 고온 안정성, 및 높은 경도를 제공한다[7]. 이러한 특성 덕분에 CFRCs는 항공기와 우주선의 부품에 널리 활용되고 있으며, 특히 고온 환경에서의 파괴인성 및 내열성에서 뛰어난 성능을 발휘한다[8]. SiC 매트릭스는, 고온 환경에서 우수한 파괴인성을 제공하며, 부식 및 열 충격에 강한 특성을 갖는다[9]. 그러나 높은 취성으로 인해 가공된 표면에서 균열이나 계면 분리와 같은 결함이 발생할 수 있으며, 이는 부품의 성능 저하와 수명 단축으로 이어질 수 있다[10].
SiC 매트릭스의 한계를 극복하기 위해, 최근에는 MAX phase 세라믹을 매트릭스로 사용한 연구가 활발히 진행되고 있다. MAX phase는 고온 안정성, 높은 경도 및 고온에서의 균열 자가 치유(crack healing) 특성을 제공하는 세라믹 소재로, 이를 사용하면 SiC 매트릭스의 취성 문제를 보완할 수 있다[11]. 특히 [TeX:] $$\mathrm{C}_{\mathrm{f}}-\mathrm{SiC}$$ 복합재료를 [TeX:] $$\mathrm{C}_{\mathrm{f}}-\mathrm{MAX}$$ phase 또는 [TeX:] $$\mathrm{SiC}_{\mathrm{f}}-\mathrm{MAX}$$ phase 복합재료로 대체할 경우, 이들 복합 재료는 균열에 대한 취약성을 줄이고, 극한 환경에서도 더 높은 안정성을 제공할 수 있다. 이로 인해 MAX phase는 항공우주와 같은 고온 및 고압 환경에서 활용 가능성이 높은 소재로 평가된다.
MAX phase 중에서 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ 구조는 M-site에 다양한 전이 금속 원소를 적용하여 물성과 활용 범위를 확장할 가능성이 크다. 연구에 따르면, [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$의 부피 탄성계수(bulk modulus)는 M-C 단일 탄화물의 부피 탄성계수와 비례하며, 부피 탄성계수가 클수록 외부 압력에 대한 변형이 적고 강성이 높아 극한 환경에서도 내구성을 향상시킨다[12]. 연구에 따르면, [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$보다 부피 탄성계수가 큰 M-site 원소들이 관찰되었다. 이는 새로운 소재 개발에 중요한 단서를 제공한다.
MAX phase 중에서도 [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$는 매트릭스로 사용하기에 특히 유망한 소재로 주목받고 있다. [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$는 우수한 산화 저항성과 균열 억제 능력을 보이며, 고온 환경에서도 기계적 성능을 유지할 수 있다[13]. 이 소재는 반복적인 하중과 열적 응력 하에서도 균열 전파를 효과적으로 억제하며, 섬유-매트릭스 계면의 마찰력을 감소시켜 복합재의 장기적인 내구성을 향상시킨다[14]. [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$ 매트릭스를 도입한 복합재는 고온 산화 환경에서도 뛰어난 성능을 발휘하며, [TeX:] $$\mathrm{TiO}_2$$ 보호층을 형성하여 탄소섬유를 효과적으로 보호함으로써 극한 환경에서 안정성을 유지한다[15]. 이러한 특성은 [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$가 복합재 매트릭스로서 항공우주 분야에서 요구되는 우수한 성능을 제공할 수 있는 유망한 소재임을 시사한다[16,17].
MAX phase는 전이금속 원소의 종류에 따라 강도, 경도, 열전도도, 열팽창계수가 달라지며, 이를 통해 [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$ 외에도 다양한 MAX phases들이 극한 환경에서 높은 안정성과 우수한 기계적 특성을 제공할 수 있는 가능성을 보여준다[18]. UHTC에서 Zr, Hf, Ta 원소는 주요 후보군으로 활용되며, ZrC, [TeX:] $$\mathrm{HfB}_2$$ 등의 형태로 많이 연구되고 있다[19, 20]. 이들 전이금속 기반 화합물은 내산화성이 높고, 극한환경에서 우수한 안정성을 보이기 때문에 이를 포함한 MAX phase를 CFRCs 매트릭스로서 활용될 가능성이 있다. 그러나 현재 MAX phase 연구는 주로 [TeX:] $$\mathrm{Ti}_2 \mathrm{AlC},$$ [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$와 같은 Ti계 MAX phase에 집중되어 있으며, Zr, Hf, Ta와 같은 전이 금속을 포함한 MAX phase는 합성의 어려움으로 인해 연구된 데이터가 부족한 상황이다[21,22]. 이에 본 연구에서는 다양한 전이금속이 포함된 MAX phase를 극한 환경에서의 CFRCs 매트릭스 후보로 고려하고, 그 활용 가능성을 탐색하고자 한다.
특히, 준조화 근사법(Quasi-harmonic Approximation, QHA)을 도입한 ab initio 계산을 활용하여 기존 실험에서 구현하기 어려운 물성을 보다 비용 효율적으로 예측하고 신속하게 계산함으로써, [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase의 구조적 안정성과 기계적 특성을 체계적으로 분석하였다. 이를 바탕으로, 극한 환경에서의 응용 가능성을 구체적으로 검토하고, CFRCs 매트릭스로서의 적합성을 평가하였다[23].
2. 계산 방법
[TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$의 구조와 기계적 특성 및 열적 안정성을 확인하기 위한 전자밀도이론(DFT) 기반 ab initio calculation 계산은 Vienna ab initio simulation package (VASP) 코드를 기반으로 진행되었다[24]. 전자와 원자핵 간 거리에 따른 전자 분포 확률 변화를 고려하기 위해 generalized gradient approximation with the Perdew-Burke-Ernzerhof(GGA-PBE) exchange correlation functional을 교환 상관관계 에너지 식으로 사용하였다[25]. 이 때 높은 에너지 수준의 planewave까지 고려하기 위해 cutoff energy 값은 500 eV를 사용하였으며, 모든 구조의 최적화는 원자간 작용하는 힘이 0.015 [TeX:] $$\mathrm{eV} / \AA$$ 이하인 동시에 전자 에너지가 [TeX:] $$10^{-6}$$ eV 이하로 안정될 때까지 진행되었다[26].
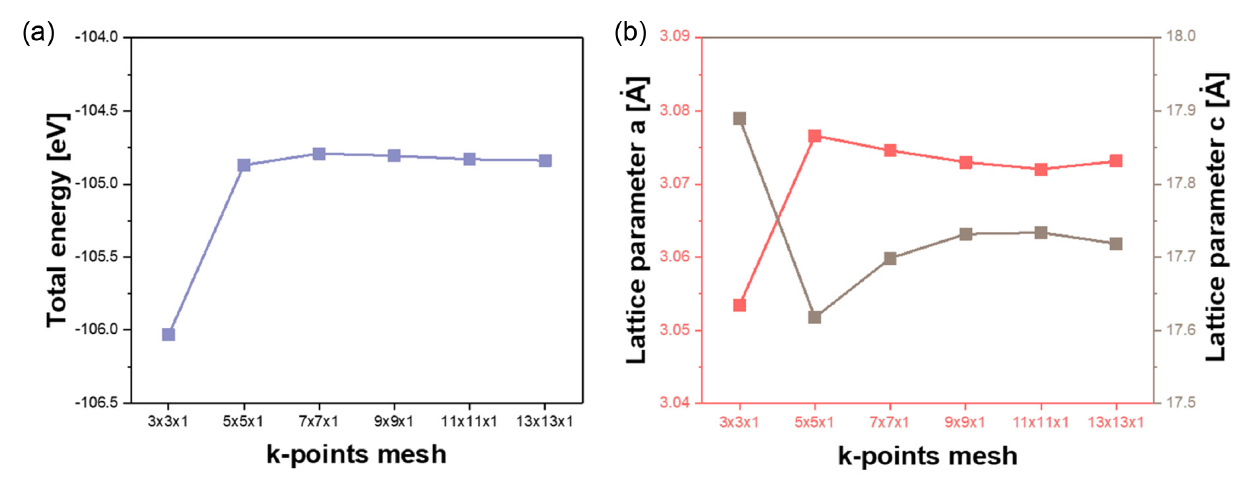
k-points 조건으로의 수렴 여부는 계산결과를 고려하여 최적의 값을 설정하였다. Figure 1에 나타낸 바와 같이, [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$ 모델로 진행된 총 에너지(total energy)와 격자상수(lattice parameter)의 변화를 관찰하여 도출된 최적 값을 지정하였다. 단위격자(unit cell)의 경우 최적 k-points mesh인 7×7×1를 가지고 계산을 진행하였다. 탄성계수 계산에서는 보다 정확한 결과를 얻기 위하여 이보다 높은 k-points mesh가 사용되었다. 적분은 Gaussian을 사용하여 수행되었다[27].
Figure 1.
변형률-응력 관계는 MAX phase의 탄성 특성을 계산하는 데 사용된다[28]. 그런 다음 6개의 변형 값(±0.005, ±0.007, ±0.009)는 탄성 상수의 정확도를 높이기 위해 + 및 − 방향으로 각 최적화된 모델에 제공된다. 이 연구에서는 육각형 구조를 고려하므로 6개의 탄성 상수([TeX:] $$\mathrm{C}_{11}, \mathrm{C}_{12}, \mathrm{C}_{13}, \mathrm{C}_{33}, \mathrm{C}_{44}, \mathrm{C}_{66}$$)는 다음과 같이 Voigt-Reuss-Hill 체계와 함께 사용되며 이를 수식 (3)−(11)에 적용해 기계적 물성을 구하였다[29,30].
(1)
[TeX:] $$E_{\text {form }}^{M_3 \text {SiC}_2}=\frac{E_{\text {total }}^{M_3 \text {SiC}_2}-\left[3 E_{\text {solid }}^M+E_{\text {solid }}^{S i}+2 E_{\text {solid }}^C\right]}{6}$$
(2)
[TeX:] $$E_{\text {cohe }}^{M_3 S i C_2}=\frac{E_{\text {total }}^{M_3 S i C_2}-\left[3 E_{\text {atom }}^M+E_{\text {atom }}^{S i}+2 E_{\text {atom }}^C\right]}{6}$$
(8)
[TeX:] $$G_R=5 C^2 C_{44} C_{66} \div\left\{6 B_V C_{44} C_{66}+2 C^2\left(C_{44}+C_{66}\right)\right\}$$
위의 식에서 [TeX:] $$E_{\text {total }}^{M_3 S i C_2}$$는 MAX phase의 화학식 단위에 따른 시스템의 에너지를 말한다. 또한 [TeX:] $$E_{\text {solid }}^M, E_{\text {solid }}^{S i}, E_{\text {solid }}^C$$는 각 원소의 가장 안정한 상태에서의 에너지를 의미하며, [TeX:] $$E_{\text {atom }}^M, E_{\text {atom }}^{S i}, E_{\text {atom }}^C$$는 각 원소의 개별 원자 상태의 에너지를 말한다. [TeX:] $$B_V, B_R, G_V, G_R$$는 각각 Voigt, Reuss으로 계산된 부피 탄성계수와 전단 탄성계수이며, 최종적인 [TeX:] $$B_H, G_H, E_H$$ 값은 Hill 식으로 나타내었다.
MAX phase의 탄성 및 열 팽창 특성의 온도 의존성을 얻기 위해 QHA를 적용하였다. 이 방법은 모델의 평형 부피가 특정 온도의 영향을 받는다고 가정한다. 이를 위해 0 K의 기저 상태 부피에서 완전히 에너지적으로 최적화된 구조를 출발점으로 삼는다. 이후 일정 부피를 변화시키며 5가지 다른 부피 조건에서 에너지-부피 곡선을 계산하였다. 따라서 격자 매개변수와 원자 위치는 전자 에너지를 최소화하여 최적화한다[31,32]. Grüneisen 상수가 2인 Debye-Grüneisen 이론을 사용하여 Helmholtz 자유 에너지를 조사하는 데 활용되며, 이 과정에서 다양한 온도 조건(최대 1500 K)을 채택한다[33].
자유 에너지 E(V)는 특정 부피 V에서 다음과 같이 표현된다. 본 연구에서는 계산된 5개의 다른 부피 조건에서의 데이터의 경향성을 효과적으로 반영하기 위하여 경험적으로 도출된 피팅 함수인 수식 (12)을 사용하였다. 수식 (12)은 데이터의 비선형적 특성을 고려하여 다음과 같이 구성되었다.
여기서 a부터 e까지는 피팅 매개변수로, 널리 사용되는 선형 EOS 중 하나인 5개의 매개변수와 함께 쓰이는 Birch-Murnaghan(BM5) EOS을 통해 최적화되었다[34,35].
비평형 깁스 자유 에너지 [TeX:] $$G(x, P, T)$$는 총 전자 에너지 [TeX:] $$E_{t o t}(x),$$ 압력과 부피 효과 [TeX:] $$P V(x),$$ 및 온도 및 엔트로피에 따른 추가 항 [TeX:] $$A_{t o t}(x, T)$$을 포함하여 다음과 같이 계산된다[36].
여기서 [TeX:] $$A_{t o t}(x, T)$$는 내부 에너지와 엔트로피의 다양한 기여를 포함하며 다음과 같이 정의된다.
[TeX:] $$E_D \text { 와 } S_D$$는 Debye 진동격자로부터 얻어진 내부 에너지와 엔트로피이며, [TeX:] $$E_{e l} \text { 과 } S_{e l}$$는 전자적 기여에 의한 내부 에너지와 엔트로피를 의미한다. 하지만, 본 연구에서 고려한 온도 범위 내에서는 전자적 기여가 거의 상수에 가까워 그 영향이 미미하며, 이를 포함할 경우 계산 복잡성이 크게 증가한다. 또한, 관련 선행 연구에서도 유사한 온도 범위 및 시스템에서는 전자적 기여가 거의 무시될 수 있다는 결과가 보고되었다[37]. 이러한 이유로 본 연구에서는 계산의 효율성을 위해서 이들을 제외하고 계산하였다.
3. 결과 및 고찰
[TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase의 상 안정성을 연구하기 위해 형성 에너지를 수식 (1)을 사용해서 계산한 결과, Cr, Mo, W를 제외한 나머지 원소들은 MAX phase를 형성할 가능성이 존재함을 발견하였다. 계산된 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase의 형성에너지, 응집에너지, 격자상수 a, 격자상수 c/a 비율이 Table 1에 나타나 있다. 형성에너지는 화합물이 형성될 때 방출되거나 흡수되는 에너지를 나타내며, 음의 형성 에너지는 화합물이 열역학적으로 안정적임을 의미한다. Ti, Zr, Hf은 낮은 형성 에너지를 통해 안정적인 화합물을 형성하며, 이는 고온 환경에서도 구조적 안정성을 유지할 가능성이 높다[38]. 반면 Cr, Mo, W는 형성 에너지가 양의 값을 가지며, 이는 해당 조성이 불안정한 MAX phase를 형성함을 의미한다. 응집에너지는 수식 (2)를 사용하여 구했다. 이는 원자들 간 결합 강도를 나타내며, 낮은 응집에너지는 강한 결합력을 의미한다. Ta은 낮은 응집에너지를 통해 강한 결합과 열적 안정성을 보이며, 열 충격이나 고온 환경에서도 안정적인 특성을 나타낸다[39].
격자상수를 바탕으로 계산된 c/a 비율은 결정 구조 안정성을 나타내는 중요한 지표로, 단위 셀의 높이(c)와 기저면의 한 변 길이(a)의 비율로 정의된다. 일반적으로 312 MAX phase의 c/a 비율은 약 6 정도이며 본 연구에서 구한 MAX 조성들의 구조는 이론적 모델과 대체로 일치한다[40]. c/a값이 1.732를 초과할 경우, [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$와 같은 MAX phase 세라믹에서 kink band 형성 조건이 충족된다[41]. kink band가 형성되면 응력이 한 방향으로 집중되지 않고 분산되어 파괴 저항성이 향상된다. 또한, 층상구조를 가진 재료에서 kink band가 전단 변형을 흡수함으로써 균열 전파를 억제하는 역할을 하는 것으로 알려져 있다[42]. 따라서 kink band의 형성은 재료의 기계적 강도와 파괴저항성을 증가시키는 데 중요한 역할을 한다. 기계적 강도와 파괴 저항성을 향상시키는 데 중요한 역할을 한다. 본 연구에서 분석된 MAX phase 조성의 c/a 비율은 모든 원소에서 1.732를 초과하여 kink band 형성이 가능함을 보여주었다.
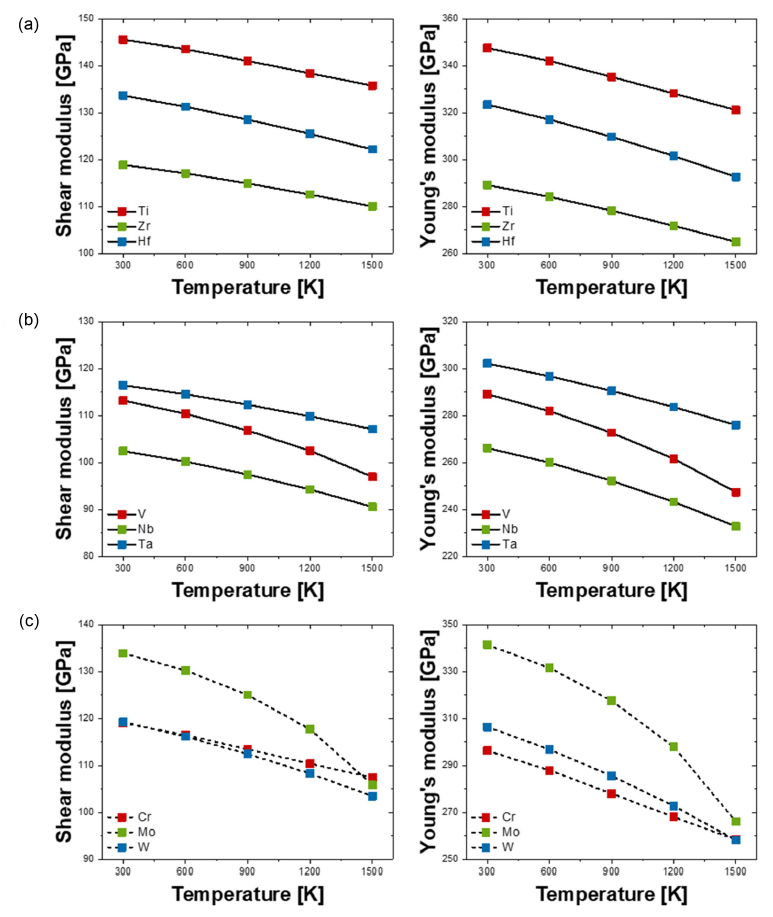
계산된 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase의 (a) 부피 탄성계수, (b) 전단 탄성계수(shear modulus), (c) 영률(Young’s modulus) (d) 경도(hardness)가 Figure 2에 나타나 있다. MAX phase의 기계적 물성치를 이전 연구 결과와 비교한 결과, 약 4% 이내의 차이를 보였으며, 이를 통해 측정값이 큰 편차 없이 신뢰할 수 있는 수준임을 확인하였다[43]. 일반적으로 고온 및 고압 환경에서는 압력에 대한 저항성을 나타내는 부피 탄성계수가 높을수록 유리하며, 균열 억제를 위해서는 인장 및 압축 응력의 분포를 결정하는 영률이 높은 것이 중요하다.
부피 탄성계수는 CFRCs의 온도에 따른 부피 탄성계수 180−205 GPa와 비교하여 전반적으로 높은 값을 보였으며, 특히 Ti는 높은 전단 탄성계수와 영률을 바탕으로 우수한 내구성과 열적 안정성을 나타내었다[44]. 이는 균열 발생 가능성이 높은 환경에서도 높은 열적 안정성을 제공할 수 있음을 시사한다. 반면, Nb는 상대적으로 낮은 전단 탄성 계수와 경도를 보여 균열 저항성이 낮다는 것을 시사한다.
Table 1.
| M composition | Formation energy (eV/atom) | Cohesive energy (eV/atom) | Lattice parameter a ([TeX:] $$\AA$$) | Lattice parameter c ([TeX:] $$\AA$$) | c/a ratio |
|---|---|---|---|---|---|
| Ti | -0.788 | -6.961 | 3.075 | 17.704 | 5.76 |
| V | -0.461 | -6.620 | 2.931 | 17.087 | 5.83 |
| Cr | 0.002 | -5.504 | 2.884 | 16.515 | 5.73 |
| Zr | -0.787 | -7.378 | 3.345 | 18.823 | 5.63 |
| Nb | -0.505 | -7.478 | 3.149 | 18.209 | 5.78 |
| Mo | 0.026 | -6.585 | 3.092 | 17.511 | 5.66 |
| Hf | -0.825 | -7.496 | 3.299 | 18.563 | 5.63 |
| Ta | -0.479 | -8.091 | 3.152 | 18.078 | 5.74 |
| W | 0.233 | -7.426 | 3.117 | 17.348 | 5.57 |
Figure 2.
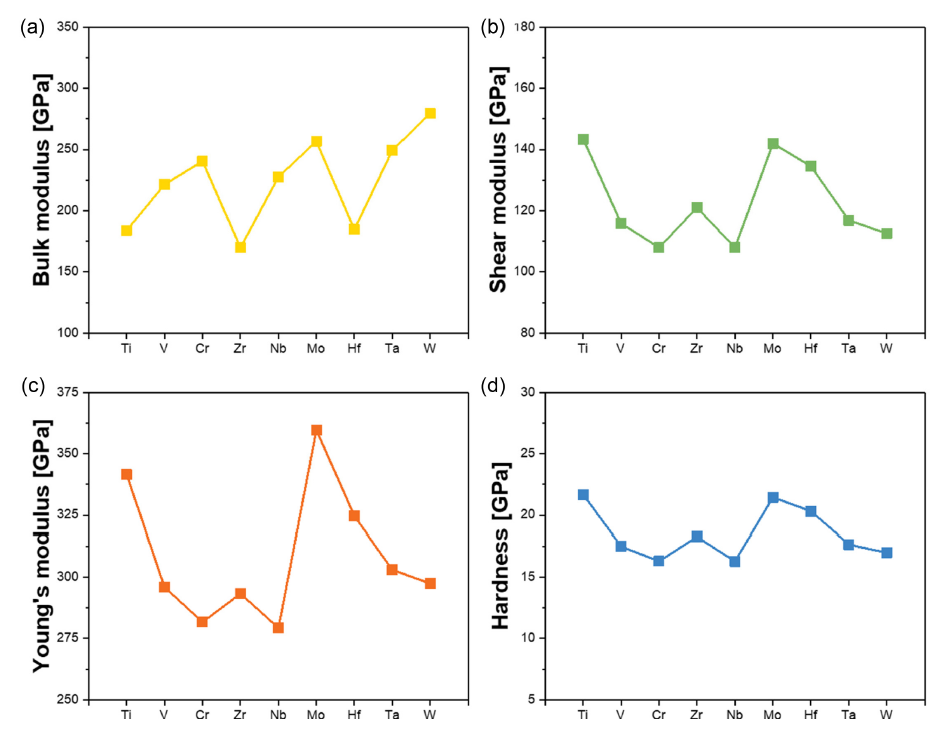
Figure 3은 M3SiC2 MAX phase 조성의 각 조성별 에너지-부피 관계를 나타내며, 300 K에서 1500 K까지 다양한 온도에서 계산된 에너지-부피 곡선을 보여준다. 동일한 조성을 가지더라도 부피에 따라 에너지가 변화한다. 이는 특정 조건에서 가장 안정한 상태를 예측하는 데 중요한 정보를 제공한다. 또한, 원자 반지름이 증가함에 따라 부피와 에너지의 관계가 변화할 수 있다. 이로 인해 특정 조건에서 안정한 상의 특성이 달라질 수 있다. 이는 원자 반지름이 결정 구조의 상대적 안정성뿐만 아니라 열역학적 성질에도 영향을 미친다[45]. 결론적으로, 에너지-부피 곡선은 원자 반지름과 조성에 따른 열역학적 안정성을 평가하는데 중요한 데이터를 제공한다. 이를 통해 가장 안정한 상태를 예측할 수 있다.
Figure 3.
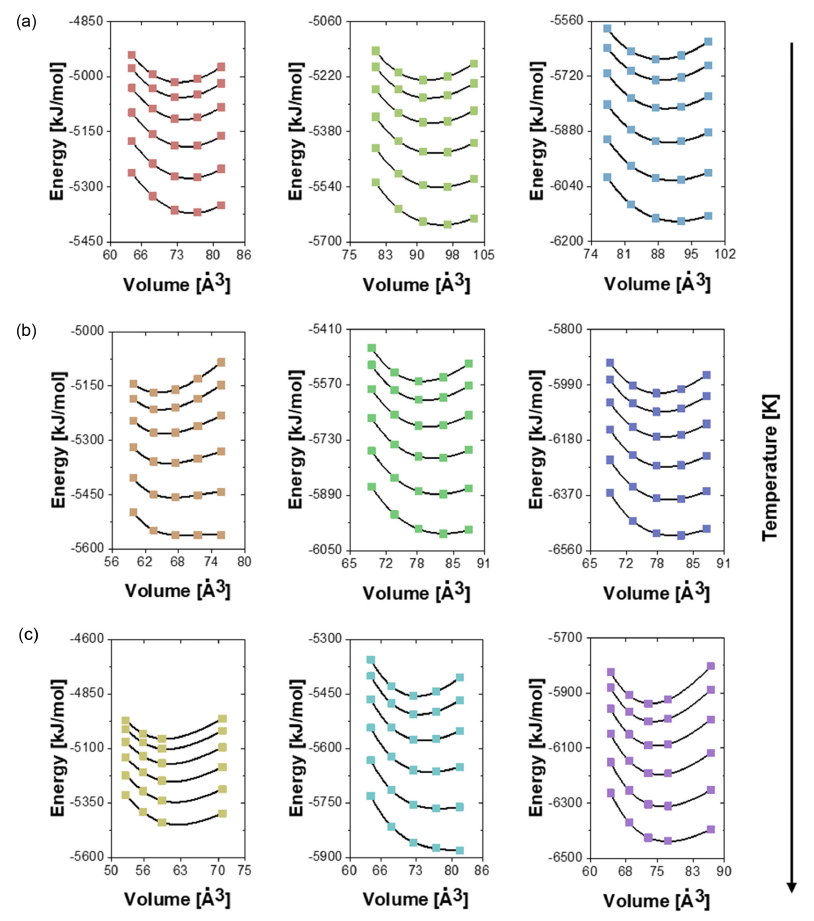
Table 2의 부피 탄성계수(B)는 외부 압력에 대한 압축 저항성을 나타낸다[46]. Zr과 Hf를 제외하고 다른 전이금속 MAX phase matrix는 [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$ matrix보다 우수한 부피 탄성 계수를 가진 것을 통해 외부 압력에 대한 변형 감소를 기대할 수 있고 다른 전이금속 원소들을 이용한 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ matrix의 적용 가능성을 확인할 수 있었다. 그리고 [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$는 상온과 비교하였을 때, 1500 K에서 30 GPa 내외의 부피 탄성 계수의 감소가 발생하였고 다른 전이 금속 MAX phase matrix 대부분 상온에 비해 1500 K에서 부피 탄성계수가 마찬가지로 30 GPa 외로 감소하는 것을 보아 충분히 [TeX:] $$\mathrm{Ti}_3 \mathrm{SiC}_2$$와 같이 MAX phase 코팅으로 구조적으로 적용해볼 수 있을 것이다. 따라서 주기가 증가할수록 결합에 관여하는 전자 밀도가 증가함으로 인해 부피 탄성계수는 증가한다[47,48].
Table 2.
| T (K) | Ti | Zr | Hf | V | Nb | Ta | Cr | Mo | W |
|---|---|---|---|---|---|---|---|---|---|
| 300 | 191.53 | 172.61 | 188.56 | 216.46 | 228.37 | 255.50 | 237.86 | 256.18 | 289.40 |
| 600 | 187.12 | 168.27 | 183.37 | 210.83 | 220.33 | 248.91 | 229.44 | 246.55 | 279.60 |
| 900 | 181.70 | 163.09 | 177.31 | 203.63 | 210.30 | 241.31 | 219.61 | 232.87 | 268.08 |
| 1200 | 176.03 | 157.45 | 170.65 | 195.02 | 198.61 | 232.91 | 209.65 | 213.67 | 255.01 |
| 1500 | 170.41 | 151.42 | 163.36 | 183.90 | 185.14 | 223.60 | 200.01 | 182.65 | 240.04 |
전단 탄성계수와 영률은 재료의 기계적 성질을 평가하는 중요한 지표이다. 이는 원자간 결합 강도에 영향을 받는다. 본 연구에서는 Table 1의 cohesive energy 값과 Figure 2의 영률 및 전단 탄성계수 간의 관계를 분석하여, 대부분의 전이금속 원소에서 유사한 경향성을 보이는 것을 확인하였다. 예를 들어, Cr, V와 같은 원소는 cohesive energy 값이 높으며, 이에 따라 영률과 전단 탄성계수 값이 상대적으로 낮은 것으로 나타났다. 반면, Ti, Hf와 같은 경우에는 cohesive energy 값이 낮고, 영률과 전단 탄성계수 값이 높은 것을 확인할 수 있었다. 다만, 모든 전이금속 원소가 동일한 경향성을 보이는 것은 아니지만, 대부분의 원소에서 일관된 패턴이 확인되었다. 해당 물성들이 금속 원소의 조성 변화에 따라 계산된 값을 Figure 4에 나타내었다. 두 기계적 물성 모두 4족 금속원소(Ti, Zr, Hf)가 5족 금속원소(V, Nb, Ta)보다 높은 값을 보였다. 이는 결합의 강도와 변형에 대한 저항성을 반영하며, 단일 전자가 채워진 오비탈의 개수가 적은 4족 금속원소가 전자 간 반발력이 낮아 강한 결합을 형성하기 때문이다. 이로 인해 4족 금속원소는 5족 금속원소에 비해 높은 전단 탄성계수와 영률 값을 가진다. 이러한 강한 결합력과 높은 융점은 고온 환경에서 우수한 내열성을 발휘하며, 금속 변형과 기계적 성질의 저하를 최소화한다. 따라서, 이러한 특성으로 인해 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase 구조에서 M-site로는 4족 금속원소가 5족 금속원소보다 적합하다는 결론을 도출할 수 있다.
Figure 4.
푸아송 비(Poisson’s ratio)는 물질의 취성-연성 거동을 나타내는 중요한 지표로, Figure 5에 나타난 바와 같이, 금속 원소의 조성 변화에 따라 그 값이 달라진다. 일반적으로 0.26 이상일 경우 연성이 높은 것으로 평가되며, 0.26 미만일 경우에는 취성 경향을 나타낸다[49]. 물질의 취성과 연성은 물질 내부에서 나타나는 화학 결합의 특성과 종류에 따라 결정된다. 취성 정도가 높은 물질은 주로 강한 공유 결합을 가지는 반면, 연성이 높은 물질은 금속 결합이 지배적으로 나타나는 특징을 보인다. Figure 5에서 분석된 결과에 따르면, 5족 금속 원소가 4족 금속 원소보다 높은 연성을 나타냈으며, 이는 전이금속의 d 오비탈에 채워지는 전자 수의 차이에 기인한다. VEC(value of electron concentration)이 증가할수록 초과된 전자가 공유 결합을 하지 않고 물질 내 금속 원소 사이에 d-d 오비탈 혼성 궤도를 생성한다. 이러한 d-d 오비탈 혼성 궤도의 생성은 금속 결합이 증가한다는 의미이며, 이는 물질의 연성 정도를 높이는 데 기여한다.
Figure 5.
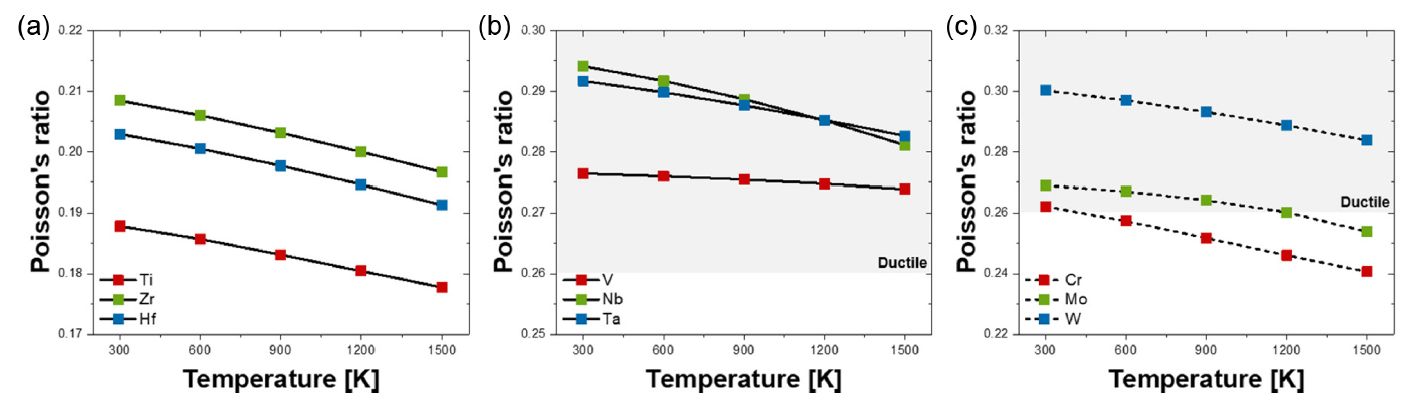
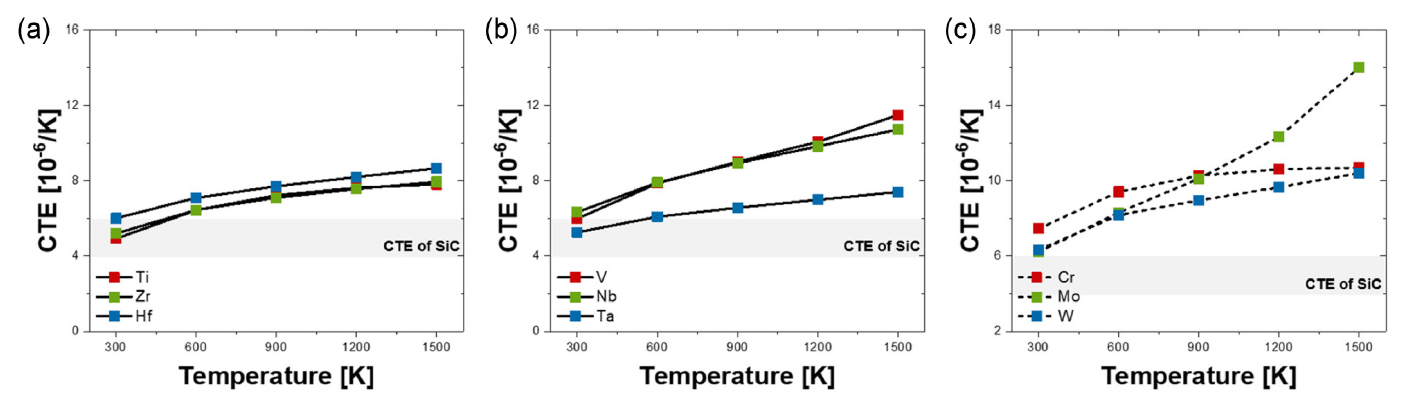
Figure 6에 나타난 바와 같이, 금속 원소의 조성 변화와 온도 조건에 따라 CTE 값이 달라진다. SiC의 CTE는 회색 영역으로 표시되어 있으며, SiC와의 CTE 차이가 적을수록 열응력이 감소한다. 이는 고속 비행 중 발생할 수 있는 급격한 온도 변화에도 재료가 균열이나 손상없이 우수한 성능을 유지할 것으로 예상된다. Figure 6(a)에서 세 금속 원소 모두 SiC와 유사한 CTE 값을 보여 열응력이 적을 것으로 예측되었다. Figure 6(b)에서 Ta는 V와 Nb보다 SiC에 가장 근접한 CTE를 나타내어 약 300 K에서 600 K의 온도 범위에서 안정적인 열팽창 특성을 보였다. 따라서 M3SiC2 구조의 M-site에 Ti, Zr, Hf, Ta와 같은 원소를 사용하면 두 재료 간 CTE 차이로 인해 발생할 수 있는 열응력을 효과적으로 완화할 수 있다. 이는 열응력으로 인한 재료의 손상을 줄이고 피로를 감소시켜, 고온 환경이나 급격한 온도 변화에서도 재료의 수명을 연장하는데 기여할 수 있을 것으로 판단된다.
4. 결 론
본 연구에서는 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase 구조의 기계적 및 열적 특성을 평가하기 위해 형성 에너지, 탄성계수, 열팽창계수 등의 물리적 특성을 체계적으로 분석하였다. 이를 통해 다양한 전이금속 조성의 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ 구조가 항공우주 및 고온 환경에서 매트릭스 재료로 활용될 가능성을 검토하였다.
형성 에너지 분석 결과, Cr, Mo, W 기반의 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase는 양의 형성 에너지를 보이기 때문에 화합물 형성이 어렵다. 기계적 특성 분석 결과, Ta 기반의 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase는 높은 부피 탄성계수로 압력 변화에 강하고, Ti, Hf 기반의 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase는 높은 전단 탄성계수와 영률로 균열 억제와 열적 내구성이 우수한 것으로 나타났다.
전반적으로 모든 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase는 높은 부피 탄성 계수와 낮은 감소율을 보여 고온 및 고압 환경에서 안정적인 성능을 제공할 수 있을 것으로 기대된다. 푸아송 비 분석 결과, V, Nb, Ta는 푸아송 비가 0.26 보다 높아 연성이 뛰어나고, 변형에 대한 저항성이 큰 것으로 나타났다. SiC와의 CTE 차이가 적을수록 열응력이 감소하여, Ti, Zr, Hf, Ta 기반의 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ 조성은 급격한 온도 변화에서도 열응력과 열적 피로를 효과적으로 완화할 수 있는 재료임을 확인하였다.
추가적으로, 기존 CFRCs의 매트릭스로 사용되던 SiC매트릭스는 높은 취성으로 인해 가공된 표면에서 균열이나 계면 분리와 같은 결함이 발생할 가능성이 있다. 이는 부품의 성능 저하 및 수명 단축으로 이어진다. 반면, SiC 대신 312 MAX phase를 매트릭스로 사용할 경우, 기존 SiC의 취성으로 인한 구조적 결함을 줄일 수 있다. 또한, 장기간의 고온 환경에서도 안정적인 성능을 유지할 수 있는 가능성이 높다. 따라서, 312 MAX phase를 매트릭스로 사용할 경우 고온 환경에서 안정성을 유지하기 때문에 기존 SiC 매트릭스의 한계를 보완할 수 있는 대안으로 적합하다고 판단하였다.
결론적으로, 본 연구에서 분석된 조성들 중 Ti, Zr, Hf, Ta 기반의 [TeX:] $$\mathrm{M}_3 \mathrm{SiC}_2$$ MAX phase는 강도, 열적 안정성, 연성, 및 열응력 완화 특성을 모두 충족하는 가장 유망한 조성으로 평가된다. 기존 연구에서 상대적으로 소홀히 다루어졌던 Ti 외 다른 전이금속을 포함하는 MAX phase 소재에 대한 기초 연구의 필요성을 확인하였다[50]. 이를 극복하기 위해 본 연구에서는 Ab initio 계산을 활용하여, 실험적으로 접근이 어려운 극한 환경 하에서의 기계적 및 열적 특성을 정량적으로 분석하였다. 이러한 접근은 기존의 실험적 한계를 보완하며, 소재의 성능 예측 및 안정성 평가에 있어 새로운 기준을 제시하는 데 기여하였다. 고온, 고압 등 첨단 산업 분야에서의 소재 응용 확대에 기여하여, 향후 다양한 MAX phase 소재의 설계 및 최적화에 기여할 것으로 기대된다.
감사의 글
이 논문은 2023년도 산업통상자원부 및 산업 기술평가관리원(KEIT) 연구비 지원에 의한 연구임(20024463).
References
- 1 B. Rapp, "Materials for Extreme Environments" , Mater. Today, 2006, 9, 6.custom:[[[-]]]
- 2 P . Gradl, O. R. Mireles, C. Katsarelis, T. M. Smith, J. Sowards, A. Park, P . Chen, D. C. Tinker, C. Protz, T. Teasley, D. L. Ellis, and C. Kantzos, "Advancement of Extreme Environment Additively Manufactured Alloys for Next Generation Space Propulsion Applications" , Acta Astronaut., 2023, 211, 483−497.custom:[[[-]]]
- 3 D. K. Schreiber, R. Schwaiger, M. Heilmaier, and S. J. McCormack, "Materials Properties Characterization in the Most Extreme Environments", MRS Bull., 2022, 47, 1128− 1142.custom:[[[-]]]
- 4 G. Karadimas and K. Salonitis, "Literature Review of Fatigue Life Performance of Ceramic Materials" , Adv. Manuf. Technol. XXXV , 2022, 25, 127−134.custom:[[[-]]]
- 5 N. P . Padture, "Environmental Degradation of High-temperature Protective Coatings for Ceramic-matrix Composites in Gas- turbine Engines" , npj Mater. Degrad., 2019, 3, 11.custom:[[[-]]]
- 6 E. Pakdel, S. Kashi, R. Varley, and X. Wang, "Recent Progress in Recycling Carbon Fiber Reinforced Composites and Dry Carbon Fiber Wastes", Resour. Conserv. Recycl., 2021, 166, 105340.custom:[[[-]]]
- 7 S. Tang and C. Hu, "Design, Preparation and Properties of Carbon Fiber Reinforced Ultra-high Temperature Ceramic Composites for Aerospace Applications: A Review" , J. Mater. Sci. Technol., 2017, 33, 117−130.custom:[[[-]]]
- 8 B. Parveez, M. I. Kittur, I. A. Badruddin, S. Kamangar, M. Hussien, and M. A. Umarfarooq, "Scientific Advancements in Composite Materials for Aircraft Applications: A Review", Polymers, 2022, 14, 5007.custom:[[[-]]]
- 9 R. H. Jones, L. Giancarli, A. Hasegawa, Y . Katoh, A. Kohyama, B. Riccardi, L. L. Snead, and W. J. Weber, "Promise and Challenges of SiC f /SiC Composites for Fusion Energy Applications" , J. Nucl. Mater., 2002, 307−311, 1057−1072.custom:[[[-]]]
- 10 Q. An, J. Chen, W. Ming, and M. Chen, "Machining of SiC Ceramic Matrix Composites: A Review", Chin. J. Aeronaut., 2021, 34, 540−567.custom:[[[-]]]
- 11 M. S. Alam, M. A. Chowdhury, T. Khandaker, M. S. Hossain, M. S. Islam, M. M. Islam, and M. K. Hasan, " Advancements in MAX Phase Materials: Structure, Properties, and Novel Applications" , RSC Adv., 2024, 14, 26995−27041.custom:[[[-]]]
- 12 C. M. Fang, R. Ahuja, O. Eriksson, S. Li, U. Jansson, O. Wilhelmsson, and L. Hultman, "General Trend of the Mechanical Properties of the Ternary Carbides M 3 SiC 2 (M = transition metal)" , Phys. Rev. B, Uppsala, 2006, 74, 054106.custom:[[[-]]]
- 13 X. Ma, X. Fan, Z. Wang, J. You, L. Cheng, and L. Zhang, "Abnormal Mechanical Hysteresis Behavior of Tyranno-ZMI SiC/SiC Containing Ti 3 Si(Al)C 2 ", J. Eur. Ceram. Soc., 2023, 43, 5904−5914.custom:[[[-]]]
- 14 H. Zhang, Z. G. W ang, Q. S. Zang, Z. F . Zhang, and Z. M. Sun, "Cyclic Fatigue Crack Propagation Behavior of Ti 3 SiC 2 Synthesized by Pulse Discharge Sintering (PDS) Technique", Scr. Mater., 2003, 49, 87−92.custom:[[[-]]]
- 15 R. Zhang, H. Zhang, F. Liu, M. Sun, and S. Ma, "High Temperature Oxidation Resistance Behavior of Ti 3 SiC 2 /Cu Composites under Migration of Ti and Cu Atomic", Ceram. Int., 2024, 50, 49490−49500.custom:[[[-]]]
- 16 E. Tabares, M. Kitzmantel, E. Neubauer, A. J. Morales, and S. A. Tsipas, "Sinterability, Mechanical Properties and Wear Behavior of Ti 3 SiC 2 and Cr 2 AlC MAX Phases" , Ceramics, 2022, 5, 55−74.custom:[[[-]]]
- 17 C. Du, B. Lei, Y . Qi, R. Zhang, and F . Liu, "Synthesis, Fabrication, and Applications of Ti 3 SiC 2 /SiC Ceramics: A Review" , J. Mater. Sci., 2024, 59, 13365−13392.custom:[[[-]]]
- 18 E. Wu, Y . Zhang, M. Li, Y. Li, K. Liang, S. Du, and Q. Huang, "The Rendering from the Periodic System of Elements on the Stability, Elastic, and Electronic Properties of M 2 AC Phases" , Materialia, 2023, 27, 101676.custom:[[[-]]]
- 19 J. F . Justin, A. Julian-Jankowiak, V . Guérineau, V . Mathivet, and A. Debarre, "Ultra-high Temperature Ceramics Developments for Hypersonic Applications", CEAS Aeronaut. J., 2020, 11, 651−664.custom:[[[-]]]
- 20 Y. Zhang, Z. Y. Fan, J. Sun, N. Li, X. Shi, and H. Li, "Effect of Transition Metal on the Structure and Oxidation Behavior of ZrB 2 (0001): Experimental and Theoretical Calculations", Comput. Mater. Sci., 2023, 226, 112213.custom:[[[-]]]
- 21 D. J. Tallman, E. N. Hoffman, E. N. Caspi, B. L. Garcia-Diaz, G. Kohse, R. L. Sindelar, and M. W. Barsoum, "Effect of Neutron Irradiation on Select MAX Phases", Acta Mater., 2015, 85, 132−143.custom:[[[-]]]
- 22 M. Haftani, M. S. Heydari, and H. R. Baharvandi, "Studying the Oxidation of Ti 2 AlC MAX Phase in Atmosphere: A Review" , Int. J. Refract. Met. Hard Mater., 2016, 61, 51−60.custom:[[[-]]]
- 23 D. Gao, Z. Shen, K. Chen, X. Zhou, H. Liu, J. Wang, Y. Li, Z. Liu, H. Deng, W . Y. Wang, and X. Zeng, "Review of Progress in Calculation and Simulation of High-temperature Oxidation" , Prog. Mater. Sci., 2025, 147, 101348.custom:[[[-]]]
- 24 G. Kresse and J. Furthmüller, "Efficiency of Ab-initio Total Energy Calculations for Metals and Semiconductors Using a Plane-wave Basis Set" , Comput. Mater. Sci., 1996, 6, 15−50.custom:[[[-]]]
- 25 J. P. Perdew, K. Burke, and M. Ernzerhof, "Generalized Gradient Approximation Made Simple" , Phys. Rev. Lett., 1996, 77, 3865−3868.custom:[[[-]]]
- 26 H. J. Monkhorst and J. D. Pack, "Special Points for Brillouin- zone Integrations, " Phys. Rev. B, 1976, 13, 5188−5192.custom:[[[-]]]
- 27 H. Kim, J. Choi, S. Park, T. Eom, K. M. Roh, and J. Kim, "Influence of Vacancies on the Stability and Mechanical Properties of V 2 AlC: Guidelines for Etching MAX Phases via ab Initio Calculations" , Ceram. Int., 2024, 50, 2652−2658.custom:[[[-]]]
- 28 M. A. Meyers and K. K. Chawla, "Mechanical Behavior of Materials" , Cambridge University Press, 2008.custom:[[[-]]]
- 29 R. Hill, "The Elastic Behaviour of a Crystalline Aggregate", Proc. Phys. Soc. A, 1952, 65, 349−354.custom:[[[-]]]
- 30 A. Reuss, "Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle", Z. Angew. Math. Mech., 2006, 9, 49−58.custom:[[[-]]]
- 31 J. George, V . L. Deringer, A. Wang, P . Müller, U. Englert, and R. Dronskowski, "Lattice Thermal Expansion and Anisotropic Displacements in α-sulfur from Diffraction Experiments and First-principles Theory" , J. Chem. Phys., 2016, 145, 234−512.custom:[[[-]]]
- 32 J. Kim and Y. J. Suh, "Temperature Dependent Elastic and Thermal Expansion Properties of W 3 Co 2 C, W 6 Co 6 C and W 4 Co 2 C Ternary Carbides" , J. Alloys Compd., 2016, 666, 262− 269.custom:[[[-]]]
- 33 X.-G. Lu, M. Selleby, and B. Sundman, "Calculations of Thermophysical Properties of Cubic Carbides and Nitrides Using the Debye-Grüneisen Model", Acta Mater., 2007, 55, 1215−1226.custom:[[[-]]]
- 34 S. L. Shang, Y. Wang, D. E. Kim, and Z. K. Liu, "First- principles Thermodynamics from Phonon and Debye Model: Application to Ni and Ni3Al" , Comput. Mater. Sci., 2010, 47, 1040−1048.custom:[[[-]]]
- 35 J. Kim and S. Kang, "First Principles Investigation of T emperature and Pressure Dependent Elastic Properties of ZrC and ZrN using Debye-grüneisen Theory" , J. Alloys Compd., 2012, 540, 94−99.custom:[[[-]]]
- 36 M. A. Blanco, E. Francisco, and V . Luaña, "GIBBS: Isothermal- isobaric Thermodynamics of Solids from Energy Curves Using a Quasi-harmonic Debye Model", Comput. Phys. Commun., 2004, 158, 57−72.custom:[[[-]]]
- 37 J. Kim, "Applicability of Special Quasi-random Structure Models in Thermodynamic Calculations Using Semi-empirical Debye-Grüneisen Theory" , J. Alloys Compd., 2015, 650, 564− 571.custom:[[[-]]]
- 38 N. A. Ganie, S. A. Mir, and D. C. Gupta, "Tantalum Half- Heusler Alloys RbTaSi and RbTaGe: Potential Candidates for Desirable Thermoelectric and Spintronic Applications", RSC Adv., 2023, 13, 7087−7101.custom:[[[-]]]
- 39 M. J. Gasch, D. T. Ellerby, and S. M. Johnson, "Ultra High Temperature Ceramic Composites", Handbook of Ceramic Composites, 2005, pp.197−224.custom:[[[-]]]
- 40 M. W. Barsoum, "The M N+1 AX N Phases: A New Class of Solids" , Prog. Solid State Chem., 2000, 28, 201−281.custom:[[[-]]]
- 41 H. J. Rathod, T . Ouisse, M. Radovic, and A. Srivastava, "Room Temperature Crack-healing in an Atomically Layered Ternary Carbide" , Sci. Adv., 2021, 7, eabg2549.custom:[[[-]]]
- 42 M. W. Barsoum, L. Farber, and T. El-Raghy, "Dislocations, Kink Bands, and Room-temperature Plasticity of Ti 3 SiC 2 ", Metall. Mater. Trans. A, 1999, 30, 1727−1738.custom:[[[-]]]
- 43 Y. Ching, Y. Mo, S. Aryal, and P . Rulis, "Intrinsic Mechanical Properties of 20 MAX‐Phase Compounds" , J. Am. Ceram. Soc., 2013, 96, 2292−2297.custom:[[[-]]]
- 44 F. Aguado and V . G. Baonza, "Prediction of Bulk Modulus at High Temperatures from Longitudinal Phonon Frequencies: Application to Diamond, c-BN, and 3C-SiC", Phys. Rev. B, 2006, 73, 024111 .custom:[[[-]]]
- 45 A. T . Paxton, M. Methfessel, and H. M. Polatoglou, "Structural Energy-volume Relations in First-row Transition Metals", Phys. Rev. B, 1990, 41, 8127.custom:[[[-]]]
- 46 Z. Chen, H. Tan, L. Yu, and C. Xiang, " Ab Initio Study of the Opto-electronic and Elastic Properties of MgGa x Al 2-x O 4 ", Eur. Phys. J. B, 2015, 88, 281.custom:[[[-]]]
- 47 R. L. Liu and D. Y . Li, "Electron W ork Function as an Indicator for Tuning the Bulk Modulus of MC Carbide by Metal- substitution: A First-principles Computational Study", Scr. Mater., 2021, 204, 114148.custom:[[[-]]]
- 48 Y. Pan, "W 2 AlC: A New Layered MAX Phase to Adjust the Balance between Strength and Ductility" , Mater. Today Chem., 2024, 35, 101915.custom:[[[-]]]
- 49 J. Kim, M. Kim, H. Kim, S. Park, and J. Kim, "Insights into the Ultra-high Temperature Solid Solutions Hf-Ta-C-N Quaternary System Using High-throughput Calculation", J. Mater. Res. Technol., 2023, 22, 2239−2250.custom:[[[-]]]
- 50 X. Ma, X. Fan, Z. Wang, J. You, L. Cheng, and L. Zhang, "Abnormal Mechanical Hysteresis Behavior of Tyranno-ZMI SiC/SiC Containing Ti 3 Si(Al)C 2 ", J. Eur. Ceram. Soc., 2023, 43, 5904−5914.custom:[[[-]]]