설인환
뼈대 구조와 군집 분석을 이용한 인체 마네킨의 최적 3D 모델링
Optimal 3D Modeling of Human Manikin Using Bone Structure and Cluster Analysis
In Hwan Sul
Abstract: Large-sized objects such as human manikins need a proper a priori mesh segmentation process for successful 3D printing. This paper applied well-known statistical mesh clustering functions, including k-means, k-medoids, DBSCAN, and pairwise distance. Especially, an inventive clustering metric, designated as point-to-bone distance, was proposed to take advantage of bone structure which can be acquired easily from free software such as Adobe Mixamo. Furthermore, the cut parts were oriented to the optimal directions, in which the minimal support structure was expected, using our previous work. Now any textile or apparel scientists can easily 3D-print their human manikins with arbitrary shapes and sizes with the help of python language.
Keywords: bone structure , cluster analysis , optimal 3d printing , human avatar , statistical
1. 서 론
본 연구진은 3D 프린팅 기술을 활용해 써멀 마네킨을 저렴하게 제작하는 일련의 연구를 진행 중이다. 써멀 마네킨은 의복 보온성을 정량화하는데 필요한 필수적인 장비이지만, 가격이 3억 내지 6억에 달하는 고가여서 국내에는 10여대의 장비만 활용가능한 것으로 알려져 있다[1]. 써멀 마네킨의 저가형 제작을 위한 세부 연구 주제 중에서, 첫 번째 단계가 마네킨의 외형을 3D 프린터를 이용해 출력하는 것이다. 이는 마네킨에 의복을 입힐 수 있도록 할 뿐만 아니라, 특히 마네킨 형상을 속이 빈 쉘(shell) 형태로 출력함으로써 내부에 발열 부재 또는 센서 등을 부가하여 써멀 마네킨을 구성하고자 하는 데에도 목적이 있다. 특히 본 연구는 일반인도 별다른 전문 지식 없이 단순히 파이썬 언어와 통계 함수 등을 사용하는 것만으로도 쉽게 분할 기법을 활용할 수 있는 것이 또 다른 목표이다.
통상 3D 프린터는 그 최대 용적보다 작은 물체를 출력하는 것이 일반적이다. 따라서 인체 마네킨과 같은 대형 물체를 출력하기 위해서는, 자동 또는 수동으로 마네킨 데이터를 사전에 분할하는 과정이 필요하다. 3D 프린팅에 특화된 자동 분할 기법에 대해서는 MIT의 Chopper[2]라는 알고리즘이 가장 유명하다. 이는 물체를 가로, 세로, 높이 방향으로 여러 단면으로 절단한 후, 몇 가지 평가함수를 이용해 그 중에서 가장 적절한 분할 형태를 선택하는 방법이다. 평가함수에는 좌우 대칭성, 구조 안정성, 사용자 입력 등 다양한 조건을 반영할 수 있어 최종 분할의 품질도 우수하지만, 물체를 쪼개는 경우의 수가 20여 만 번에 달하기 때문에 연산의 수가 많고[3], 지지구조 발생량에 대해서는 고려하지 않은 것이 단점이다.
3D 프린팅이 아니더라도 점 데이터 집합에 대한 점 데이터(point cloud)의 분할(clustering) 문제는 용접 로봇의 모션 플래닝, 머신 러닝 등 다양한 분야에서 필요한 주제로서, 파이썬 등 다양한 소프트웨어들을 통해 사용가능한 많은 기법들이 존재한다[4]. 그런데 이들은 대부분 거리만을 기준으로 집합을 형성하는 방식이 대부분이어서 원 형태로 모여 있는 점 데이터에 대해서는 잘 작동[5]하지만, 본 연구와 같은 인체 형상에 특화된 방법은 찾아보기 어렵고, 특히 3D 프린팅의 지지구조 발생량에 대한 고려 또한 이루어진 바가 드물다.
본 연구에서는 섬유의류 분야 종사자가 인체 마네킨과 같은 대형 물체를 3D 프린팅함에 있어서, 대중적인 파이썬 언어와 k-means 등의 잘 알려진 통계적 기법들을 활용해 쉽게 물체를 자동 분할할 수 있는 기법을 제안하고자 한다. 이를 위해 먼저 인체 데이터에 별 다른 정보 없이 k-means, k-medoids, DBSCAN 등 기본적인 통계 함수들을 적용해보고, 또한 그 한계점을 보완하기 위해 인체 뼈대 구조(bone structure)를 초기 정보로 활용하고자 한다. 기존 통계기법들은 단순히 메쉬의 꼭지점들 간의 거리를 이용해 분할을 시도하는 방식이지만, 본 연구에서는 메쉬 꼭지점과 뼈대의 위치를 상호 고려할 수 있는 6개 실수값을 이용하는 점-뼈대 거리 계산법을 새로 제안하고자 한다.
2. 이론적 배경
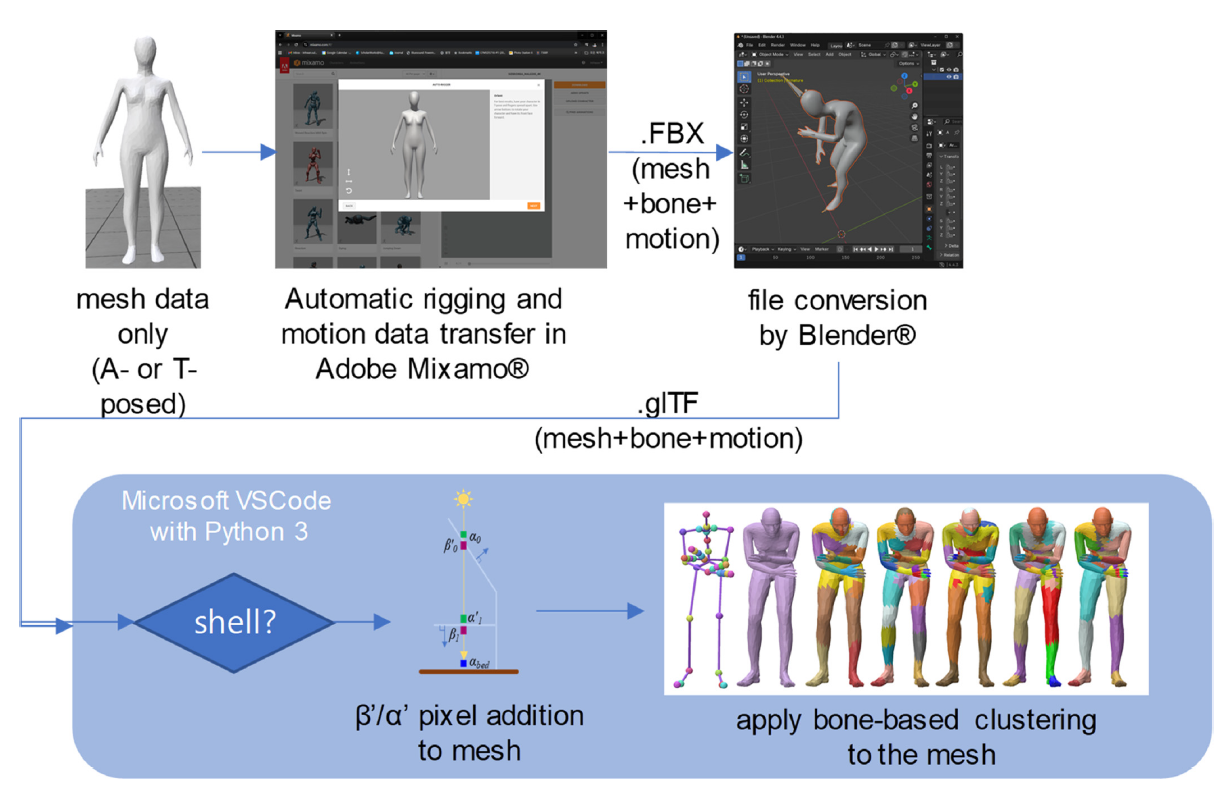
개략적인 작업 과정은 Figure 1과 같다. 사용하고자 하는 임의의 인체 메쉬 데이터에 Adobe Mixamo를 통해 뼈대 정보를 자동으로 심고, 필요한 경우 모션 데이터를 선택하여 .FBX 포맷으로 저장한다. 이를 Blender에서 .glTF 파일로 변환한 후, 주요 과정은 MS Vscode에서 자체 제작한 파이썬 코드를 통해 처리한다.
2.1. 메쉬 분할 함수
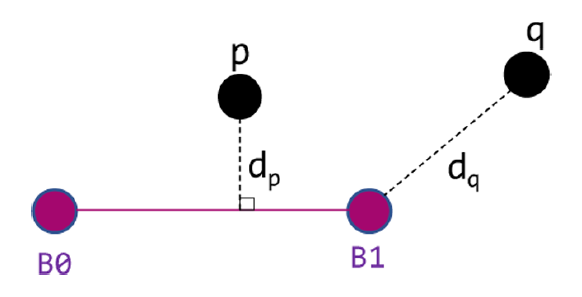
마네킨 메쉬를 적절한 크기로 분할하기 위해 잘 알려져있는 통계적 기법 중 DBSCAN, k-means, k-medoids, 쌍간 거리(pairwise-distance) 함수를 이용하였다. 또한 추가적으로 뼈대를 기준으로 삼삼각형 꼭지점의 거리를 비교하는 점-뼈대 거리(point-to-bone-distance) 기반 분할 함수를 새로 고안하였다. 이는 Figure 2와 같이 일반적인 점-선분 거리(point-to-line distance)의 계산방법[6]과 같다. 두 점(B0, B1)로 이루어지는 뼈대 구조가 있을 때, 점 p와 같이 뼈대에 내린 수선의 점이 뼈대 위에 존재하는 경우에는 수선의 길이인 dp 값을 거리값으로 사용하고, 반면 점 q와 같이 수직선이 뼈대 구간 내에 없는 경우에는 가장 가까운 뼈대점, 즉 B1과의 거리인 dq를 최종 거리값으로 사용하는 방식이다. 이를 이용하면 가장 가까이 있는 뼈대를 기준으로 메쉬를 분할할 수 있다. 다만 이를 파이썬 sklearn의 쌍간 거리 함수에 평가 기준(metric)으로 입력할 때, 삼각형 꼭지점(V)의 경우는 x,y,z 좌표가 실수 3개인 반면 뼈대 정보는 B0, B1의 x,y,z가 각각 있으므로 6개의 실수값을 가져 서로 차원이 다르다. 이를 해결하기 위해 Figure 3과 같이 꼭지점 좌표(V)는 두 번씩 반복하여 입력함으로써 6개짜리 실수 벡터(point6f)로 준비하고, 뼈대 정보는 (B0, B1)의 좌표값 한 쌍을 입력(bone6f)하여 차원을 맞춘 뒤 연산을 적용하였다.
2.2. .GLTF(.GLB) 파일을 통한 뼈대 정보 입력
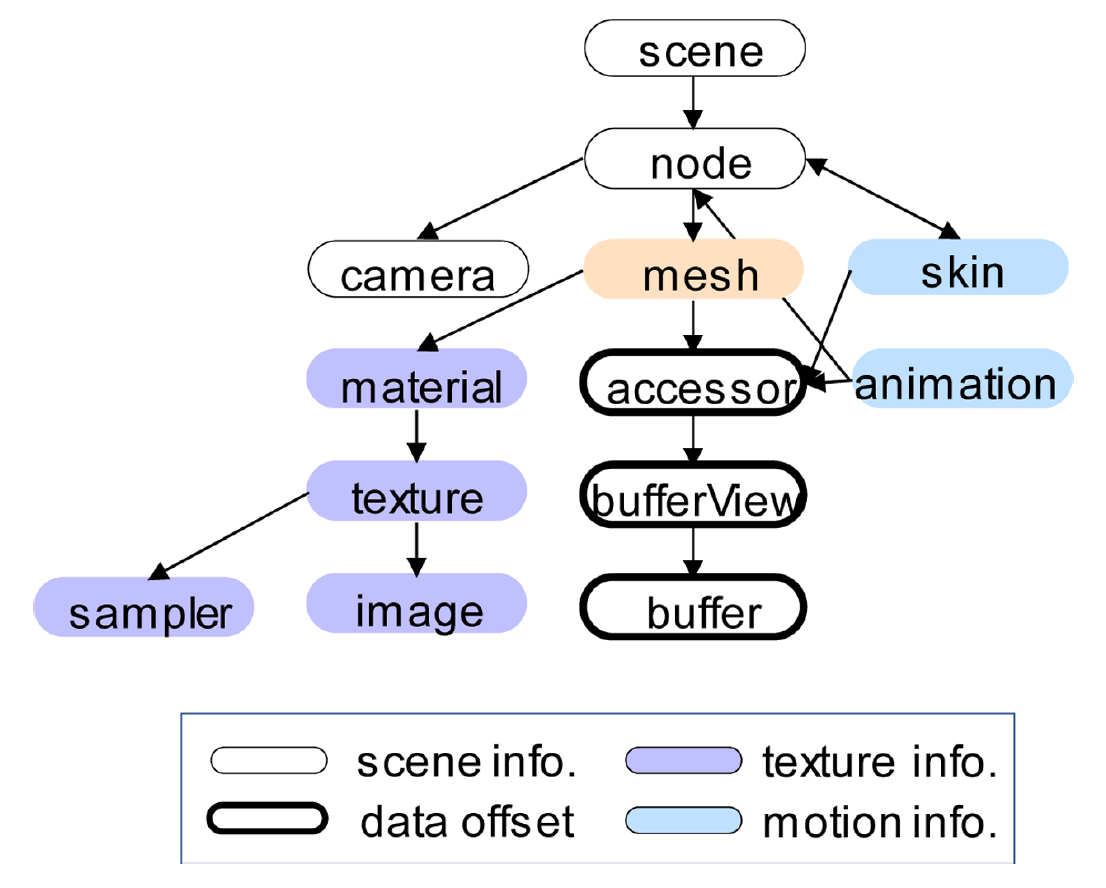
뼈대 및 모션 정보를 다룰 수 있는 3D 파일 포맷 중에서 .GLTF[7]를 이용하였다. 이 포맷은 OpenGL의 협의체인 Khronos 그룹에서 2012년 3차원 파일 포맷의 표준으로 제안한 것[7]으로서, Figure 4와 같이 다양한 형태의 데이터를 다룰 수 있도록 그래프 형태의 헤더 정보를 가지고 있다. 이 중 mesh 데이터와 material, texture, sampler, image 등 텍스쳐에 관한 부분은 일반적인 3D 파일에서도 다루던 것이지만, 최근 디지털 트윈의 활성화[8]에 대응하기 위해 인체 뼈대 정보 및 모션에 대한 정보를 담을 수 있는 skin, animation 노드가 더 포함되어 있는 것이 특징이다. 특히 이진 파일 형태로 저장하면 파일 크기를 더 줄일 수 있으며, 이 경우는 확장자를 .GLB를 사용한다. 깃허브에 Khronos 그룹의 공식 파이썬 glTF 파이썬 패키지가 공개되어 있기는 하나, 뼈대 및 모션 부분의 구현이 빠져 있어서 본 연구에서는 highfestiva[9]의 소스코드를 개조해 파일 입출력을 구현하였다.
Figure 4.
2.3. 지지구조 발생량 계산
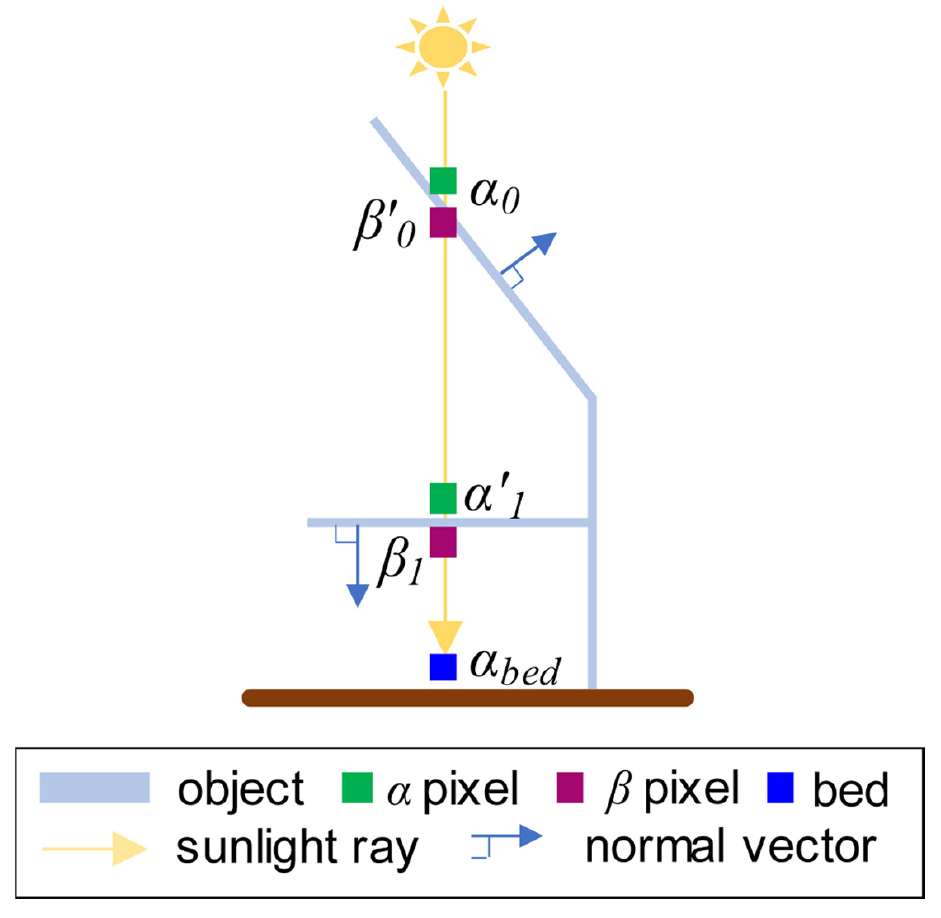
마네킨 메쉬 또는 그 조각들에 대한 3D 프린팅 시 필라멘트 소모량은 이전 연구[10]에서 개발한 알고리즘을 그대로 이용하였다. Figure 5는 계산방법을 그림으로 나타내고 있다. 기본적인 아이디어는 물체를 -Z 방향으로 픽셀화하여 픽셀 개수를 이용해 부피를 계산하는 것으로서, 특히 물체의 삼각형 메쉬가 닫히지 않은 쉘인 경우에는 특별히 Figure 5와 같이 알파 픽셀과 베타 픽셀이 서로 짝을 이루도록 픽셀을 추가하는 방법을 이용하였다. 이후 부위별 충진계수와 필라멘트 밀도 등을 곱하면 부위별 및 전체 필라멘트 질량을 계산할 수 있다.
3. 실 험
3.1. 3D 프린터
(주)신도리코의 FDM 방식 3D 프린터 DP-202와 PLA 필라멘트를 출력 대상으로 가정하였다. 이 프린터의 최대 출력 크기는 200×200×189 mm3이다. 지코드 생성 시 베드 고정 옵션은 래프트(raft) 형상을, 내부채움과 지지구조 형상은 직선형으로 하였으며, 기타 파라미터들은 기본 설정된 값을 그대로 이용하였다.
3.2. 메쉬 데이터
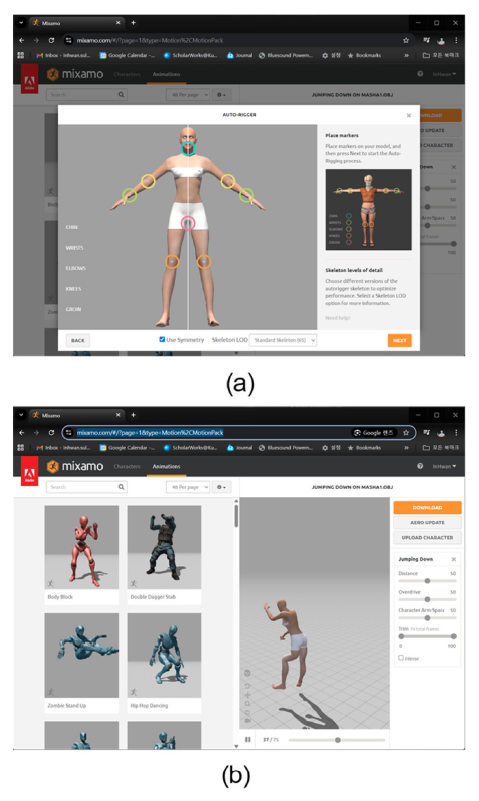
A형 정적 포즈를 가진 원본 인체 마네킨 데이터를 Wavefront .OBJ 포맷(삼각형 13,672개)으로 온라인 사이트(Turbosquid.com)에서 구매하였다. 여기에 뼈대 구조를 자동 생성하기 위해 Adobe Mixamo 홈페이지[12]에서 턱, 가랑이, 팔꿈치, 손목, 무릎 등의 특징점을 마우스로 클릭하여 지정(Figure 6a)하였다. 이 때 손 부위 뼈대의 자유도를 선택할 수 있는데, 뼈대가 한 부위에 몰려 있을 경우 분할이 과다하게 진행될 수 있으므로, 손가락이 없는 파일(no-finger)과 손이 두 개의 가지 형태로 되어 있는 파일(2-finger)를 각각 생성하였다. 이후 기본 구비된 모션 중 Jumping Down을 선택한 다음 .FBX 파일로 내보내기 하였다(Figure 6b). Blender(버전 4.4.3) 소프트웨어에서 아바타의 키를 171 mm로 조정한 뒤 .GLTF 포맷으로 저장하여 사용하였다.
3.3. SW 및 HW
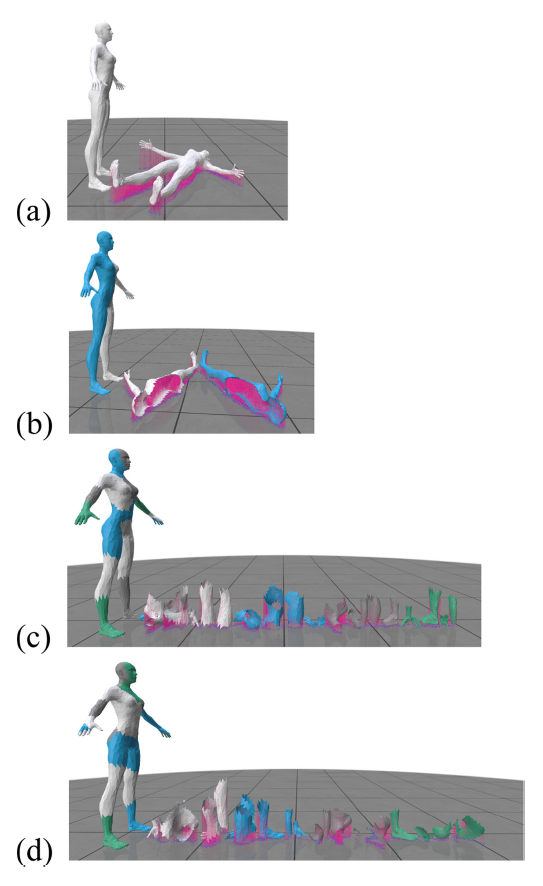
Microsoft Visual Studio Code (버전 1. 103.1)에서 파이썬 기반으로 소스코드를 작성하되, 3D 렌더링용으로는 polyscope 패키지[13]를, 메쉬의 쉘 변환은 meshlib 패키지의 OffsetMesh 기능을, 메쉬 분할 통계 처리는 sklearn, scipy, trimesh패키지의 내장 함수를 이용하였다. Figure 7은 최종 작성된 파이썬 코드의 실행 화면 사례이며, 가장 왼쪽의 텍스쳐가 입혀진 마네킨이 원본 메쉬 데이터이고, 나머지 서 있는 아바타들은 통계 기법에 의해 분할된 결과들이다. 이들 분할된 아바타들 앞 쪽 바닥에 놓인 조각들은 이전 연구에서 개발한 C++ DLL[10]을 이용해 3D 프린팅 시 지지구조량이 최소가 되는 배향으로 회전시킨 것이며, 자주색 픽셀들은 지지구조를 의미한다. 중저가형과 고급형 하드웨어에서의 실행 속도를 비교하기 위해 Table 1과 같이 가격별 두가지의 CPU를 사용해 연산속도를 측정하였다. 개발된 소스코드는 Microsoft의 Github[14]를 통해 공유하였다.
Figure 7.

Table 1.
| ID | Product name | Base/max clock (GHz) | # of cores/threads | Singleprecision TFLOPs† |
|---|---|---|---|---|
| CPU1 | AMD Ryzen5 7500f | 3.7/5.0 | 6/12 | 1.3 |
| CPU2 | AMD Ryzen9 7950X | 4.3/5.7 | 16/32 | 1.8 |
†: Tera FLoating point Operation Per Second.
4. 결과 및 고찰
4.1. 정적 포즈일 때
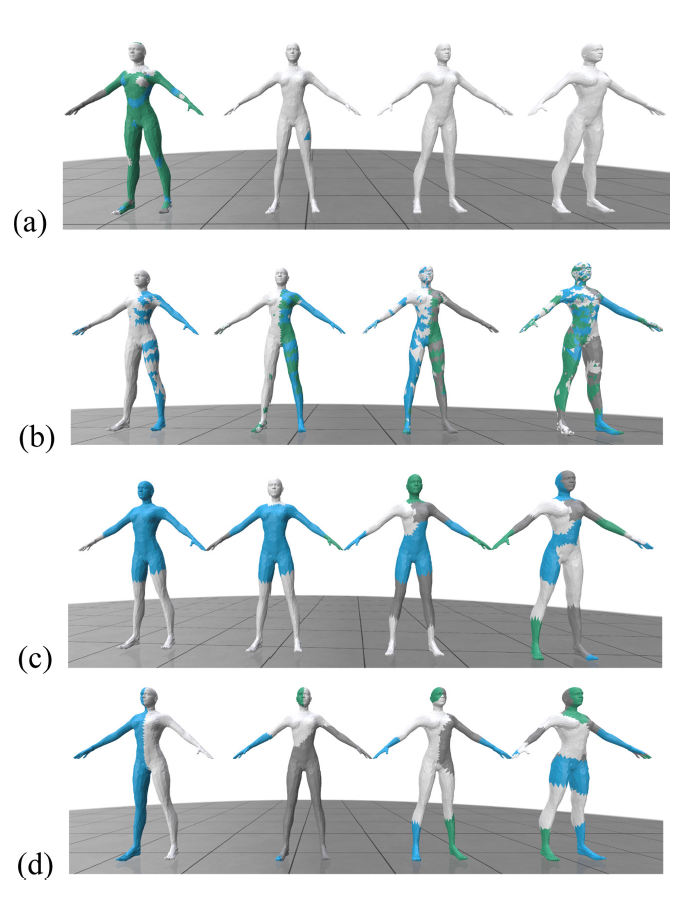
먼저 3D 인체 스캔에 있어 가장 많이 쓰이는 A형 정적 포즈를 가진 아바타를 대상으로 분할을 실시하였다. 여러 분할 방법 중 먼저 Figure 8a와 같이 sklearn의 DBSCAN[15]을 먼저 테스트하였는데, 이는 입력 인자로 거리값(일명 eps; 본 연구에서는 k로 호칭함)과 이 거리 내에 있는 최소점의 수를 입력하게 된다. Figure 8a는 거리값으로 2, 5, 10, 20 mm를 각각 입력한 결과이고, 이 때 최소 점의 수는 5개로 하였다. 잘 알려져 있는 바와 같이 DBSCAN이 eps 값에 매우 민감[16]하며, 본 연구에서도 Figure 8a과 같이 k=5 이상인 경우에는 분할이 제대로 이루어지지 않아 실용성이 낮아 보인다.
Figure 8b는 군집 분석 기법 중 대표적인 k-means[17]를 적용한 결과이다. 함수는 trimesh 패키지에 있는 k-means()를 이용했으며, 입력 인자로는 원하는 군집의 개수(k)를 정수로 입력한다. k 값을 2, 5, 10, 20으로 각각 입력했을 때 최종 군집의 개수는 각각 3, 5, 8, 15개가 형성되었으나, Figure 8b와 같이 군집들이 또렷하게 형성되지 않고 서로 산포되어 형성되었다. 이는 k-means가 초기 무게중심과 노이즈에 크게 민감하여 전역해(global optimal)보다는 국소해(local optimal)에 잘 빠지는 것이 원인[5]으로 보인다.
다음으로는 Figure 8c와 같이 sklearn의 병합 군집(agglomerative clustering) 함수[18]를 적용하였는데, 입력 인자(k)는 마찬가지로 원하는 군집의 개수이다. 입력 k 값 2, 5, 10, 20에 대해 군집의 개수가 3, 6, 11, 21개로 형성되었으며, 앞의 k-Means에 비해서는 훨씬 더 깔끔한 분할 결과를 보여주였다.
마지막으로 Figure 8d는 sklearn의 k-medoids[19]를 적용한 결과이다. k-means가 군집의 무게 중심을 구하기 위해 평균을 이용하는 반면, k-medoids는 중간점(medoid)을 이용함으로써 노이즈에 덜 민감한 것이 장점으로 알려져 있다[5]. 본 연구에서도 Figure 8d와 같이 적용된 네 가지 군집 기법 중 가장 만족스러운 분할 결과를 보여주었다. 그러나 Figure 8d의 허벅지와 허리가 같은 부위로 연결되어 있는데, 이러한 부분은 지지구조 발생의 원인이 될 수 있다.
Figure 8.
다만 k-medoids는 k-means에 비해 연산량이 다소 많은 것이 단점으로 알려져 있는데, 이와 관련하여 적용된 네 가지 분할 기법에 대해 그 수치적인 연산 결과를 Table 2에 나타내었다. 여기서 k는 입력 인자, #은 분할된 조각의 개수, [TeX:] $$1 / \mu / \sigma$$은 분할된 조각들의 길이/평균/표준편차를 의미하며, [TeX:] $$M_{s s}$$는 Figure 5의 알고리즘으로 예측한 지지구조의 무게 값이다. DBSCAN의 경우는 Figure 8a에서 확인한 바와 같이 조각의 수가 일정치 않거나 노이즈가 너무 많이 발생하였고, 이에 따라 조각 길이의 표준편차도 90을 넘는 큰 값을 보였다. 나머지 k-means, 병합군집, k-medoids는 조각의 개수에 있어서는 k 값과 선형적으로 비례하는 경향을 보였으나, k-means의 경우 마찬가지로 조각 길이의 편차가 컸고, k-medoids만이 k 값이 10을 넘어갈수록 편차가 20이하로 감소하는 결과를 보였다. 이는 그다지 작은 값이라고 볼 수 없지만, 사용된 이들 네 가지 분할 함수들은 파이썬 환경에서 매우 쉽게 사용할 수 있는 것이 장점으로 보인다. Figure 9는 네 가지 분할 방법 중 가장 편차값이 작을 때의 조건을 하나씩 선택하여 비교한 것이다. 각 아바타 앞에 높인 조각들은 최적 배향을 계산하여 회전된 상태이다. DBSCAN(Figure 9a)과 k-means(Figure 9b)는 입력 아바타와 동일한 길이를 가지므로 분할의 의미가 없고, 병합 군집(Figure 9c)과 k-medoids(Figure 9d)는 3D 프린팅 분할 출력 목적에 적합해 보인다.
Table 2.
| k | DBSCAN | k-means | Agglomerative | k-medoids | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | l [mm] | Mss [g] | # | l [mm] | Mss [g] | # | l [mm] | Mss [g] | # | l [mm] | Mss [g] | |||||
| μ | σ | μ | σ | μ | σ | μ | σ | |||||||||
| 2 | 57 | 14.5 | 24.3 | 23.4 | 3 | 115.7 | 81.8 | 24.9 | 3 | 95.2 | 68.1 | 23.0 | 3 | 115.8 | 81.9 | 22.2 |
| 5 | 3 | 69.7 | 91.7 | 22.6 | 5 | 103.1 | 77.9 | 25.5 | 6 | 47.7 | 37.2 | 21.6 | 6 | 68.9 | 59.4 | 21.4 |
| 10 | 2 | 99.6 | 99.6 | 22.6 | 8 | 112.4 | 68.2 | 29.6 | 11 | 40.4 | 19.1 | 18.6 | 11 | 44.3 | 23.7 | 20.3 |
| 20 | 2 | 99.6 | 99.6 | 22.6 | 15 | 117.7 | 60.1 | 33.7 | 21 | 31.3 | 13.6 | 15.1 | 21 | 31.2 | 17.4 | 16.6 |
Figure 9.
4.2. 임의 포즈일 때
앞에서 적용한 k-medoids 등의 분할 함수는 널리 알려진 것이어서 일반 3D 프린터 사용자가 접근하기가 용이하다는 것이 장점이다. 그러나 이들은 단순히 점들 간의 거리 값을 기준으로 하기 때문에 구(sphere) 형상으로 군집되어 있는 모집단에 대해서만 좋은 결과를 얻을 수 있다[5]. 따라서 본 연구에서는 인체 형상 데이터에서 자주 사용되는 모션 데이터 내지 뼈대 구조를 추가적인 정보로 이용하였다.
뼈대 구조는 인체 3D 스캐닝 과정에서 인체 특징점을 파악하고 인체 치수를 계측하는 과정에서 부수적으로 얻어지기도 하고, 애니메이션 분야에서는 모션 캡쳐 데이터를 아바타에 입혀 인체 메쉬 데이터를 변형하기 위한 목적으로 사용된다. 과거에는 아바타와 뼈대의 크기가 다를 경우 MotionBuilder와 같은 특수한 소프트웨어를 이용해 전문가의 수작업이 필요하였으나, 최근에는 Blender의 Rokoko 스튜디오[20]처럼 딥러닝 기술을 이용해 영상으로부터 뼈대 정보와 모션 정보가 실시간으로 측정가능하기도 하다. 또한 단순히 뼈대 정보만 필요한 경우에는 Accurig[21], Mixamo 등의 무료 소프트웨어가 사용가능한데, 특히 본 연구에서는 이 중에서 설치 과정 없이 홈페이지에서 간단히 사용가능한 Adobe의 Mixamo를 이용하였다.
먼저 앞의 A형 포즈를 가진 아바타에 뼈대를 부여(Figure 10a)한 뒤, k-means, k-medoids 등의 함수를 적용할 때 이들 뼈대 위치를 초기 중심점으로 입력하여 분할을 시도한 결과가 Figure 10b-d이다. 앞의 Figure 9에는 DBSCAN과 kmeans가 제대로 분할을 하지 못했는데, 뼈대 정보를 초기 값으로 부여한 결과 k-means도 Figure 10b와 같은 양호한 분할 결과를 나타내었다. k-medoids와 쌍간 거리 기법도 Table 3의 정량적 결과처럼 뼈대 정보가 없는 Table 2의 경우보다 더 양호한 분할 결과를 보여주었다.
Figure 10.
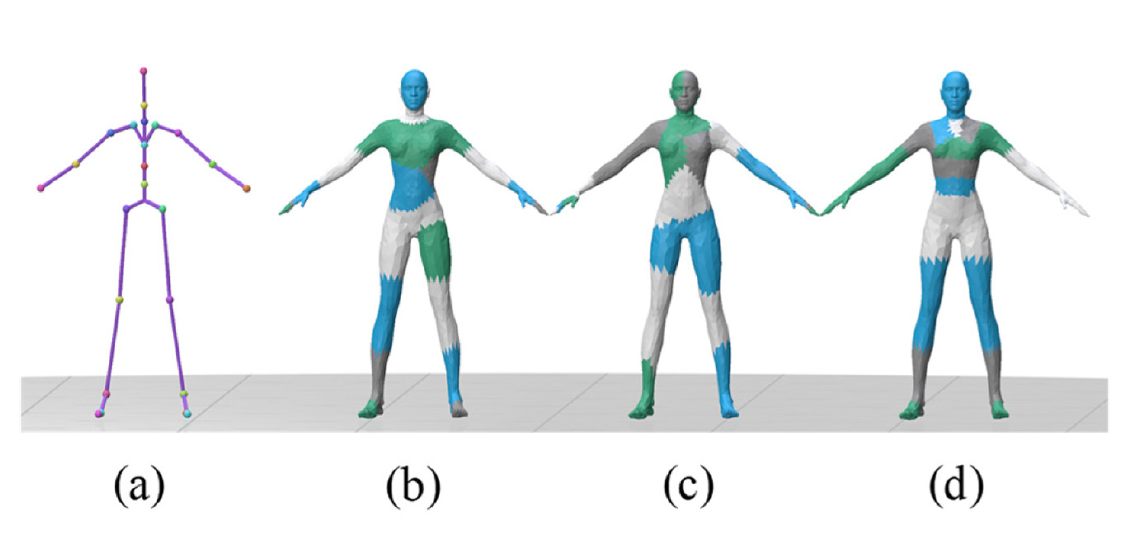
Table 3.
| Method | Cut parts | |||
|---|---|---|---|---|
| # | l [mm] | Mss [g] | ||
| μ | σ | |||
| k-means | 25 | 28.2 | 12.6 | 19.2 |
| k-medoids | 25 | 28.8 | 16.2 | 20.8 |
| Pairwise | 21 | 32.9 | 13.7 | 19.0 |
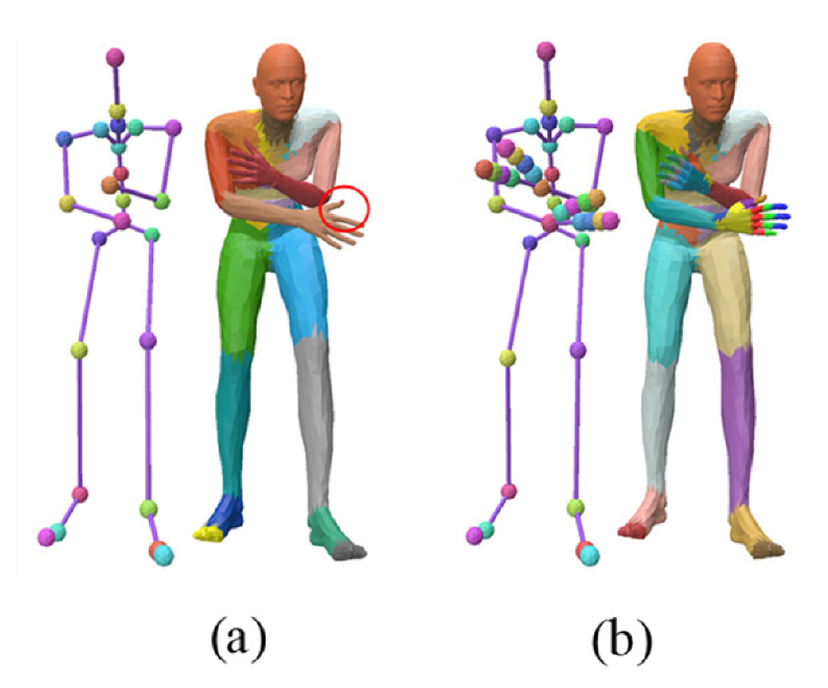
그 다음으로는 아바타의 포즈를 Jumping Down 모션의 첫 번째 프레임으로 변경하여 k-medoids 함수를 적용하였다. 그 결과 Figure 11a와 같이 대부분의 조각은 정상적으로 분할되었으나, 오른손 엄지손가락의 경우 거리값만을 기준으로 하다보니 오른손 뼈대점이 아닌 왼팔꿈치 뼈대점을 가까운 점으로 계산하여 오류가 발생하였다. 이러한 정도의 오류는 눈으로 쉽게 발견할 수 있으므로 후처리 과정에서 수작업으로 분리하여 출력을 진행할 수도 있지만, 오류 발생 확률을 줄이기 위해 Mixamo에서 손 뼈대의 개수를 8개짜리 뼈대가 두 가닥으로 나뉘어져 있는 2-finger 형태로 변경하여 사용한 결과가 Figure 11b이다. 이 경우 오른손 엄지와 같은 오류는 발생하지 않았으나, 손과 팔이 하나의 덩어리로 분할되었던 Figure 11a에 비해 조각의 수가 최대 16개로 증가하였고, 이는 3D 프린팅 후 후처리 및 접합 작업의 양을 늘리게 되는 단점이 있으므로 사용자의 선택이 필요해 보인다.
Figure 11.
최종적으로 Figure 11b의 2-finger 형태 아바타에 뼈대를 사용하지 않은 k-medoids와, 뼈대를 기반으로 하는 k-means, k-medoids, 쌍간 거리, 점-뼈대 거리 함수를 사용하여 분할을 진행한 결과가 Figure 12이다. 입력 k 값은 20으로 하였으며, Figure 12a는 Figure 11b와 같은 뼈대 구조이고, Figure 12b는 분할을 하지 않았을 때의 결과이다. 이들 분할 결과를 Table 4에 정량적으로 나타내었다. 분할하지 않은 Figure 12b의 경우 키가 107.8 mm이며 이를 최적 방향으로 회전시켰을 때의 지지구조의 양이 14.4 g으로 계산되었다. 뼈대를 사용하지 않은 k-medoids(Figure 12b)의 경우 그림 상으로는 의 A형 포즈일 때처럼 분할이 양호한 것처럼 보이지만, 실제로는 양쪽 무릎부위 등 분할되어야 할 부분들이 분리되지 않고 서로 같은 갈색 색상을 띠고 있는 것을 확인할 수 있다. 이 현상은 뼈대 기반 k-means (Figure 12d), kmedoids (Figure 12e)도 마찬가지이다. 나머지 쌍간 거리(Figure 12f), 점-뼈대 거리(Figure 12g)는 이격되어 있는 부분들이 동일한 그룹으로 검출되는 오류는 보이지 않았으며, 조각 길이의 표준편차와 지지구조 발생량 모두 쌍간 거리 (Figure 12f)가 최소값을 보였다. 다만 쌍간 거리(Figure 12f)는 두 다리가 균일한 길이로 분할되지 않은 반면, 점-뼈대 거리(Figure 12g)는 무릎을 기준으로 다리가 두 개의 조각으로 분할되어 훨씬 자연스러운 결과를 보여주였다. 따라서 실제로 인체 아바타를 뼈대 정보를 중심으로 분할하고자 하는 경우에는 쌍간 거리 또는 본 연구진이 개발한 점-뼈대 거리를 사용하는 것이 바람직해 보인다.
Figure 12.
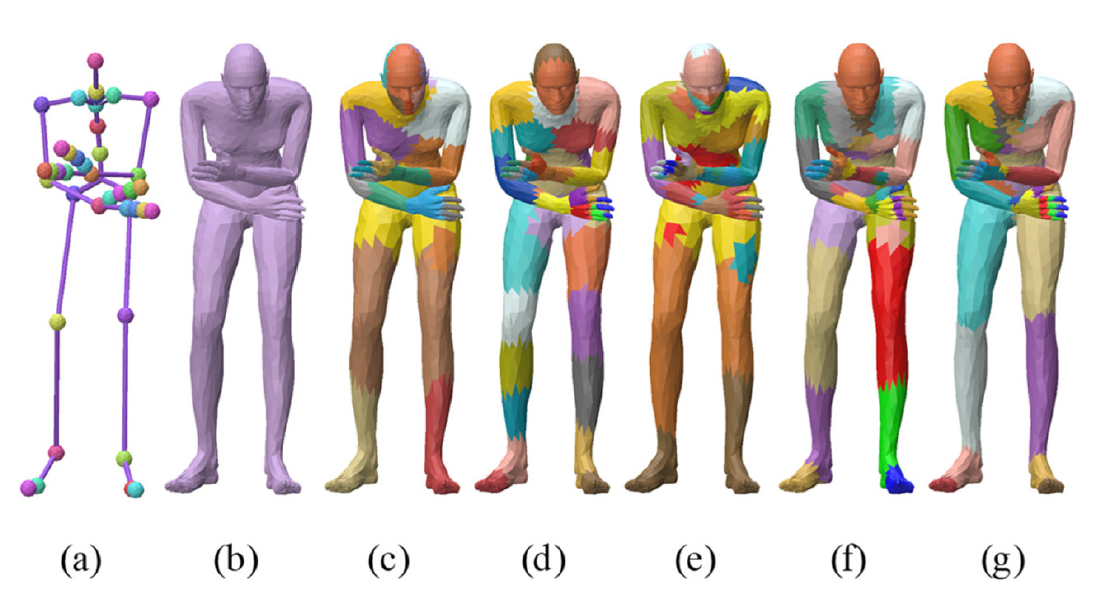
Table 4에는 알고리즘 실행시간도 나타내었다. 실행시간은 분할 시간과 최적 배향 계산 시간으로 구성되는데, 중저가형 CPU(CPU1), 고급형 CPU(CPU2) 모두 실제 분할 시간은 1초 미만이었고 나머지 20여초의 시작은 최적 배향을 계산하는 데 소모되었다. 최적 배향 탐색에 있어서는 탐색 각도 간격 [TeX:] $$10^{\circ}$$를 사용했는데, 이는 물체 조각들을 X축 기준으로 [TeX:] $$10^{\circ}$$씩, Y축 기준으로 [TeX:] $$10^{\circ}$$씩 회전시켜 가며 지지 구조 발생량을 계산한 다음 그 중에서 가장 최소한 것을 선택한다는 의미이다. 따라서 뼈대 기준 분할 방식 중에서는 조각 수가 적은 쌍간 거리가 실행시간도 작게 측정되었으나, 이는 물체 메쉬의 삼각형 개수, 선택한 분할 기법, 지지구조량 탐색 각도 간격에 따라 달라질 수 있다. 좀 더 빠른 실행 속도가 필요한 경우에는 GPU 버전[11]을 실행하면 그래픽카드 성능에 따라 최대 수십 배 단축될 수 있으나, 이 경우 정확도가 다소 떨어진다. 참고로 Chopper[2]의 경우 복잡한 C++ 언어로 속도 최적화되어 있고 사용된 군집화 기법도 매우 달라 단순 비교는 어렵지만, 인체 아바타 형상의 경우 4,700여개 꼭지점을 가진 인체 메쉬 형상에 대해 2.3분의 탐색 시간이 걸린 것으로 볼 때 통계적 기법을 이용한 본 연구의 접근법이 연산량에 있어서는 유리한 것으로 보인다.
Table 4.
| Method | Cut parts | Calc. time [sec] | |||||
|---|---|---|---|---|---|---|---|
| # | l [mm] | Mss [g] | |||||
| μ | σ | CPU1 | CPU2 | ||||
| No cut | 1 | 107.8 | 0.0 | 14.4 | 1.6 | 0.7 | |
| k-medoids | 20 | 23.3 | 12.1 | 11.0 | 24.3 | 12.2 | |
| Bone-based | k-means | 40 | 16.9 | 6.6 | 10.6 | 32.5 | 21.9 |
| k-medoids | 40 | 16.1 | 12.5 | 11.0 | 26.8 | 23.1 | |
| Pairwise distance | 34 | 18.1 | 9.7 | 10.8 | 22.3 | 18.7 | |
| Point-to-bone distance | 40 | 16.5 | 10.9 | 11.0 | 28.8 | 24.6 | |
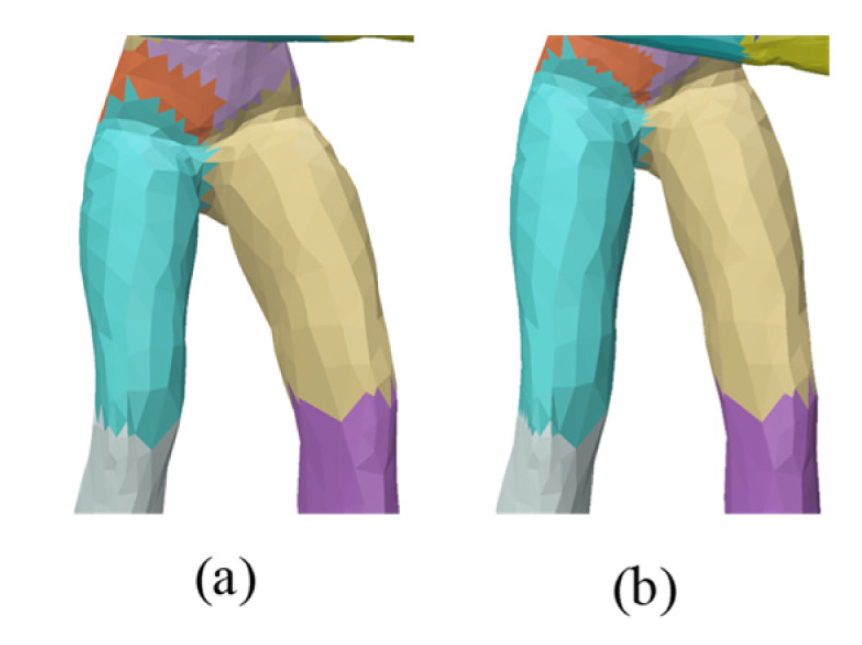
본 연구의 미진한 점으로는 실제 3D 프린팅을 통한 실험값과의 비교 과정이 이루어지지 않은 점이 있다. 이는 Figure 13과 같이 메쉬 경계면의 돌출 현상(jaggedness) 때문이다. 이를 보완하기 위해 경계면에 있는 삼각형들을 4개의 서브 삼각형으로 나눈 뒤(subdivision)하여 다시 2차 분할을 거치는 방법을 적용한 결과 Figure 13b와 같이 돌출의 정도가 줄어들기는 하였으나, 완전히 해결되지는 못하였다. 또한 본 연구에서는 뼈대 정보만을 입력값으로 하여 어느 정도 균일한 크기의 조각들을 분할하는 데에는 성공하였으나, 명시적으로 3D 프린터의 최대 용적을 고려하지는 못하였다. 이를 위해서는 본 연구에서 고안한 점-뼈대 거리 함수를 좀 더 보완해야할 것으로 보인다.
5. 결 론
본 연구는 비전문가가 소형 3D 프린터를 이용해 프린터보다 큰 크기를 갖는 아바타를 분할 출력할 수 있는 방법론을 제공하고자 한다. 아바타 데이터는 임의의 메쉬를 사용할 수 있으며, 뼈대 및 모션 데이터는 무료 홈페이지인 Adobe Mixamo를 이용하였다. 메쉬 정보와 모션 및 뼈대 정보를 전달할 수 있도록 새로 표준으로 제정된 .GLTF 포맷을 이용하였으며, 대부분의 소스코드는 파이썬을 기반으로 하여 Github를 통해 공유하였다. 뼈대 정보를 사용하지 않은 경우에도 k-medoids 함수를 사용하여 목표 조각 개수를 20 이상으로 할 경우 원활한 결과를 보여주었으나, 분할된 조각의 크기가 큰 단점이 있었다. 또한 자세가 A-포즈가 아닌 일반적인 자세인 경우에는 k-medoids 함수도 일부 부위가 잘못된 부위로 분할되는 경우가 있었다. 반면 뼈대 정보를 초기 데이터로 사용하여 분할한 결과 k-medoids의 분할 오류는 여전히 발생하였지만 쌍간 거리와 점-뼈대 거리는 길이 표준편차와 지지구조 발생량에 있어서 훨씬 양호한 결과를 보여주었다. 특히 본 연구에서 새로 제안한 점-뼈대 거리는 쌍간 거리 함수보다는 수치적으로 우수하지는 않았으나, 분할된 조각들이 등간격이어서 사용 목적에 따라서는 도움이 될 것으로 판단된다. 개발된 알고리즘을 이용할 경우 일반 3D 프린터 사용자도 전문적인 지식없이 단순히 파이썬 언어를 사용하는 것만으로도 임의의 크기를 가진 인체 마네킨 형상을 쉽게 분할 출력할 수 있을 것으로 기대된다. 특히 마네킨을 속이 빈 쉘(shell) 형상으로 출력할 경우 내부에 발열 부재 또는 센서 등을 부착할 수 있으므로 써멀 마네킨 연구에 있어서도 직접적인 도움이 될 수 있다. 다만 본 연구에서 사용한 평가 메트릭들은 거리를 기준으로 하다 보니 조각의 경계면들이 날카롭게 형성되었고, 3D 프린터의 최대 크기도 제한요소로 고려되지 못하였다. 이들은 후속 연구에서 보완될 예정이다.
References
- 1 J. Y. Jung, "Optimal 3D Printing of Organic Heating Thermal Manikin Using Human Feature Point Based Automatic Segmentation and Support Structure Tomography", Master Thesis, Kumoh National Institute of Technoogy, Gumi, 2022.custom:[[[-]]]
- 2 L. Luo, I. Baran, S. Rusinkiewicz, and W . Matusik, "Chopper: Partitioning Models into 3D-printable Parts", ACM Trans. Graph., 2012, 31, 129−137.custom:[[[-]]]
- 3 M. Nicholson, "QChopper-Segmentation of Large Surface Meshes for 3D Printing" , Queen's University, Cadana, 2016.custom:[[[-]]]
- 4 R. S. Rodrigues, J. F. Morgado, and A. J. Gomes, "Part‐based Mesh Segmentation: A Survey", Computer Graphics Forum, 2018, 37, 235−274.custom:[[[-]]]
- 5 C. Liang, J. Yin, J. Wu, J. W ang, M. Wei, and Y . Guo, " A Survey of 3D Mesh Segmentation Based on Clustering Analysis", J. Computer-Aided Design & Computer Graphics, 2020, 32, 680− 692.custom:[[[-]]]
- 6 M. M. Deza and E. Deza, "Encyclopedia of Distances", Encyclopedia of distances, Springer, 2009, pp.1−583.custom:[[[-]]]
- 7 W . Lemoine and M. Wijnants, "Progressive Network Streaming of T extured Meshes in the Binary gltf 2.0 Format" , Proceedings of the 28th International ACM Conference on 3D Web Technology, 2023, pp.1−11.custom:[[[-]]]
- 8 B. Simões, M. Del Puy Carretero, J. Sanchez, C. Toro, and J. Posada, "Digital twin and 3D web-based use cases in industry", Proceedings of the 27th International Conference on 3D Web Technology, 2022, pp.1−5.custom:[[[-]]]
- 9 https://github.com/highfestiva/gltf-skin-anim-viewer (Accessed September 1, 2025).custom:[[[https://github.com/highfestiva/gltf-skin-anim-viewer(AccessedSeptember1,2025)]]]
- 10 I. H. Sul, "Improvement of 3D Printing Support Structure Tomography by Correcting Calculation Error between Explicit and Implicit Formula" , Text. Sci. Eng., 2023, 60, 194− 200.custom:[[[-]]]
- 11 I. H. Sul and C. K. Park, " A Study on the Speed of Real-time Garment Simulation Using Particle Based Method" , Text. Sci. Eng., 2009, 46, 362−368.custom:[[[-]]]
- 12 S. Blackman, "Rigging with Mixamo", Unity for Absolute Beginners, Springer, 2014, pp.565−573.custom:[[[-]]]
- 13 https://www.polyscope.run (Accessed September 1, 2025).custom:[[[https://www.polyscope.run(AccessedSeptember1,2025)]]]
- 14 https://github.com/cfms-lab/Tomo_Shell2025 (Accessed September 1, 2025).custom:[[[https://github.com/cfms-lab/Tomo_Shell2025(AccessedSeptember1,2025)]]]
- 15 A. Beer, A. Draganov, E. Hohma, P. Jahn, C. M. Frey, and I. Figure 13. Mesh jaggedness examples; (a) our current result and (b) subdivided result.custom:[[[-]]]